이동된 로그 로지스틱 확률밀도함수
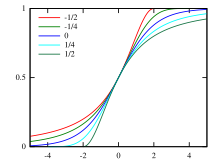
μ 0 , σ 1 {\displaystyle \ mu =0,\ displayma =1,} ma 누적분포함수
μ 0 , σ 1 {\displaystyle \ mu =0,\ displayma =1,} ma 매개변수 μ ∈ ∞ ∞ {\ displaystyle \mu \in (-\inflt ,+\inflt )\,} 위치 실제 ) σ 0 ∞ {\ displaystyle \sigma \in (0,+\infit )\,} 척도
ξ ∞ ∞ {\ displaystyle \xi \in (-\inflt ,+\inflt )\,} 모양 지원 x ⩾ μ − σ / ξ ( ξ > 0 ) {\displaystyle x\geqslant \mu -\basma /\xi \,\(\xi >0)} x ⩽ μ − σ / ξ ( ξ < 0 ) {\displaystyle x\leqslant \mu -\buffma /\xi \,\(\xi <0)}
x ∈ ( − ∞ , + ∞ ) ( ξ = 0 ) (-\displaystyle x\in (-\in)\\\\,\(\xi =0)} PDF ( 1 + ξ z ) − ( 1 / ξ + 1 ) σ ( 1 + ( 1 + ξ z ) − 1 / ξ ) 2 {\displaystyle {\frac {(1+\xi z)^{-(1/\xi +1)}{\\chma \좌측(1+(1+\xi z)^{1/\xi }\오른쪽)^
여기서 z μ σ {\ displaystyle =(x-\mu )/\ma \,} CDF ( 1 + ( 1 + ξ z ) − 1 / ξ ) − 1 {\displaystyle \left(1+(1+\xi z)^{-1/\xi }\오른쪽)^{-1}\,}
여기서 z μ σ {\ displaystyle =(x-\mu )/\ma \,} 평균 μ + σ ξ ( α csc ( α ) − 1 ) {\displaystyle \mu +{\frac {\buffma }{\xi }}}(\buffer \csc(\buffer )-1)}
여기서 α π ξ {\ displaystyle \alpha =\pi \xi \,} 중앙값 μ \displaystyle \mu \,} 모드 μ + σ ξ [ ( 1 − ξ 1 + ξ ) ξ − 1 ] {\displaystyle \mu +{\frac {\frac}{\xi }}}{1-\xi }}{1+\xi }\오른쪽)^{\xi }} 분산 σ 2 ξ 2 [ 2 α csc ( 2 α ) − ( α csc ( α ) ) 2 ] {\displaystyle {\frac{\frac {\pxi^{2}}[2\csc(\properties )-(\property \csc(\property )^{2}]}
여기서 α π ξ {\ displaystyle \alpha =\pi \xi \,}
이동 된 로그 로지스틱 분포 는 일반화된 로그 로지스틱 분포 또는 3-모수 로그 로지스틱 분포로도 알려진 확률 분포 다.[1] [2] 그것은 일반화된 로지스틱 분포라고도 불렸지만,[3] 일반화된 로지스틱 분포 를 보라라는 용어의 다른 용어와 상충된다. null
정의 이동된 로그 로지스틱 분포는 이동 매개 변수 Δ {\displaystyle \delta } 로지스틱 분포 로부터 얻을 수 있다. X {\displaystyle X} X Δ {\displaysty X+\delta } 따라서 Y {\displaystyle Y} ( Y Δ {\displaystyle \log(Y-\delta )} Shift 매개변수는 (변경되지 않은) 로그 로지스틱의 척도 및 형상 매개변수에 위치 매개변수를 추가한다. null
이 분포의 속성은 로그 로지스틱 분포의 속성에서 도출하기 쉽다. 그러나 일반화된 Pareto 분포와 일반화된 극단값 분포에 사용되는 것과 유사한 대체 매개변수화는 더 해석 가능한 매개변수를 제공하고 이들의 추정에 도움이 된다. null
이 매개변수화에서 이동된 로그 로지스틱 분포의 누적 분포 함수 (CDF)는 다음과 같다.
F ( x ; μ , σ , ξ ) = 1 1 + ( 1 + ξ ( x − μ ) σ ) − 1 / ξ {\displaystyle F(x;\mu ,\sigma ,\xi )={\frac {1}{1+\왼쪽(1+{\frace{\xi(x-\mu )}{\sigma }}{\sigma }^{-1/\xi }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} for 1 + ξ ( x − μ ) / σ ⩾ 0 {\displaystyle 1+\xi (x-\mu )/\sigma \geqslant 0} μ ∈ R {\displaystyle \mu \in \mathbb {R} } σ > 0 {\displaystyle \sigma >0\,} ξ ∈ R {\displaystyle \xi \in \mathbb {R} } 일부 참조에서는 모양을 매개 변수화하기 위해 display displaystyle \kappa [3] [4] null
확률밀도함수 (PDF)는
f ( x ; μ , σ , ξ ) = ( 1 + ξ ( x − μ ) σ ) − ( 1 / ξ + 1 ) σ [ 1 + ( 1 + ξ ( x − μ ) σ ) − 1 / ξ ] 2 , {\displaystyle f(x;\mu ,\sigma ,\xi )={\frac {\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-(1/\xi +1)}}{\sigma \left[1+\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }\right]^{2}}},} 다시 1 ξ ( x μ σ 0. {\displaystyle xi (x- )/\ma \geqslant .}
형상 매개변수 ξ {\displaystyle \xi } ξ 1 {\displaystyle \xi >1 μ μ ξ점근증 이 있다. ξ {\displaystyle x=\sigma /\ xi } x μ {\displaysty x=\mu .} .
관련 분포 μ σ ξ {\displaystyle \mu =\sigma /\xi ,} ξ {\displaystyle \xi 로지스틱 분포 로 감소한다.형상 모수 ξ 1 {\displaystyle \xi = ( ξ . {\displaystyle \xi =1 일반화된 파레토 분포 와 동일하다. } 적용들 3-모수 로그 로지스틱 분포는 홍수 빈도를 모델링하기 위해 수문학 에서 사용된다.[3] [4] [5] null
대체 매개 변수화 PDF와 CDF에 대한 간단한 표현식을 가진 대체 매개변수는 다음과 같다. 형상 매개변수 α {\displaystyle \alpha }, displaystyle beta } 및 display gamma } .
f ( x ) = α β ( x − γ β ) α − 1 ( 1 + ( x − γ β ) α ) − 2 {\displaystyle f(x)={\frac {\alpha }{\beta }}{\bigg (}{\frac {x-\gamma }{\beta }}{\bigg )}^{\alpha -1}{\bigg (}1+{\bigg (}{\frac {x-\gamma }{\beta }}{\bigg )}^{\alpha }{\bigg )}^{-2}}
CDF는 다음에 의해 제공된다.
F ( x ) = ( 1 + ( β x − γ ) α ) − 1 {\displaystyle F(x)={\bigg (}1+{\bigg)(}{\frac {\beta }{x-\gamma }}}}}^{\alpha }{\bigg )}^{-1}
The mean is β θ csc ( θ ) + γ {\displaystyle \beta \theta \csc(\theta )+\gamma } β 2 θ [ 2 csc ( 2 θ ) − θ csc 2 ( θ ) ] {\displaystyle \beta ^{2}\theta [2\csc(2\theta )-\theta \csc ^{2}(\theta )]} θ = π α {\displaystyle \theta ={\frac {\pi }{\alpha }}} [7]
참조 ^ Venter, Gary G. (Spring 1994), "Introduction to selected papers from the variability in reserves prize program" (PDF) , Casualty Actuarial Society Forum , 1 : 91–101 ^ Geskus, Ronald B. (2001), "Methods for estimating the AIDS incubation time distribution when date of seroconversion is censored", Statistics in Medicine , 20 (5): 795–812, doi :10.1002/sim.700 , PMID 11241577 ^ a b c Hosking, Jonathan R. M.; Wallis, James R (1997), Regional Frequency Analysis: An Approach Based on L-Moments , Cambridge University Press, ISBN 0-521-43045-3 ^ a b Robson, A.; Reed, D. (1999), Flood Estimation Handbook , vol. 3: "Statistical Procedures for Flood Frequency Estimation", Wallingford, UK: Institute of Hydrology, ISBN 0-948540-89-3 ^ Ahmad, M. I.; Sinclair, C. D.; Werritty, A. (1988), "Log-logistic flood frequency analysis", Journal of Hydrology , 98 (3–4): 205–224, doi :10.1016/0022-1694(88)90015-7 ^ "EasyFit - Log-Logistic Distribution" . Retrieved 1 October 2016 .^ a b "Guide to Using - RISK7_EN.pdf" (PDF) . Retrieved 1 October 2016 .
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들













![{\displaystyle \mu +{\frac {\sigma }{\xi }}\left[\left({\frac {1-\xi }{1+\xi }}\right)^{\xi }-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3234781adb448370f3a7d4073c460b630bdab66)
![{\displaystyle {\frac {\sigma ^{2}}{\xi ^{2}}}[2\alpha \csc(2\alpha )-(\alpha \csc(\alpha ))^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7608a00d698835b4f898f584eaf8983af7c6bd6c)











![{\displaystyle f(x;\mu ,\sigma ,\xi )={\frac {\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-(1/\xi +1)}}{\sigma \left[1+\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }\right]^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c96002fc1eff907617fff2d31e76d578ef5a04)












![{\displaystyle \beta ^{2}\theta [2\csc(2\theta )-\theta \csc ^{2}(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6918a7bd675bcd9b2d47da8ef6a48e8f31957f1d)



