확률분포
삼각형 확률밀도함수
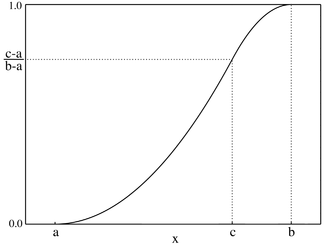
누적분포함수
매개변수 a : a ∈ ( − ∞ , ∞ ) ~a\in(-\flatty,\flatty)} b : a < b b:~a[b],} c : a ≤ c ≤ b (\displaystyle c:~a\leq c\leq b\,} 지원 a ≤ x ≤ b a\leq x\leq b\!} PDF { 0 을 위해 x < a , 2 ( x − a ) ( b − a ) ( c − a ) 을 위해 a ≤ x < c , 2 b − a 을 위해 x = c , 2 ( b − x ) ( b − a ) ( b − c ) 을 위해 c < x ≤ b , 0 을 위해 b < x . {\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{for }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b,\\[4pt]0&{\text{for }}b<x. \end{case}}} CDF { 0 을 위해 x ≤ a , ( x − a ) 2 ( b − a ) ( c − a ) 을 위해 a < x ≤ c , 1 − ( b − x ) 2 ( b − a ) ( b − c ) 을 위해 c < x < b , 1 을 위해 b ≤ x . {\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}} 평균 a + b + c 3 {\displaystyle {\frac {a+b+c}{3} }}} 중앙값 { a + ( b − a ) ( c − a ) 2 을 위해 c ≥ a + b 2 , b − ( b − a ) ( b − c ) 2 을 위해 c ≤ a + b 2 . {\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}. \end{case}}} 모드 c c\\displaystyle c\,} 분산 a 2 + b 2 + c 2 − a b − a c − b c 18 {\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}} 왜도 2 ( a + b − 2 c ) ( 2 a − b − c ) ( a − 2 b + c ) 5 ( a 2 + b 2 + c 2 − a b − a c − b c ) 3 2 {\displaystyle {\frac {{\sqrt{2}}(a\! +\!b\!-\!2c)(2a\!\!b\!c)(a\!\!\!2b\! +\!c)}{5(a^{2}\! +\!b^{2}\! +\!c^{2}\!-\!ab\!-\!ac\!\!bc)^{\frac {3}{2}}:} 엑스트라 쿠르토시스 − 3 5 {\displaystyle -{\frac {3}{5}}} 엔트로피 1 2 + ln ( b − a 2 ) {\displaystyle {\frac {1}{1}:{2}}+\ln \leftd\frac {b-a}{2}}\오른쪽)} MGF 2 ( b − c ) e a t − ( b − a ) e c t + ( c − a ) e b t ( b − a ) ( c − a ) ( b − c ) t 2 {\displaystyle 2{\frac {(b\!-\!c)e^{at}\!\!(b\!-\!a)e^{ct}\! +\!(c\!-\!a)e^{bt}{{(b-a)(c-a)(b-c)t^{2}}: CF − 2 ( b − c ) e i a t − ( b − a ) e i c t + ( c − a ) e i b t ( b − a ) ( c − a ) ( b − c ) t 2 {\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!\!(b\!-\!a)e^{ict}\! +\!(c\!-\!a)e^{ibt}{{(b-a)(c-a)(b-c)t^{2}}:
확률 이론 과 통계 에서 삼각 분포 는 하한 a , 상한 b 및 모드 c 를 갖는 연속 확률 분포 로 여기 서 < b 와 and c ≤ b 이다.
특례 바운드에서의 모드 분포 는 c = a 또는 c = b일 때 단순화된다. 예를 들어 a = 0, b = 1 및 c = 1이면 PDF 및 CDF 는 다음과 같이 된다.
f ( x ) = 2 x F ( x ) = x 2 } 을 위해 0 ≤ x ≤ 1 왼쪽. {\begin{array}{rl}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{array}\right\}{\text{{}{}}{}}}{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"{{{{{} E ( X ) = 2 3 VAR ( X ) = 1 18 {\displaystyle {\begin}\operatorname {E}(X)&={\frac {2}{3}\[8pt]\operatorname {Var}(X)&={\frac {1}{18}}\ended}}}}}}}} 두 표준 균일 변수의 절대 차이 분포 a = 0, b = 1 및 c = 0에 대한 이 분포는 X = X1 - X 의2 분포인데, 여기서 X 1 , X 는2 표준 균일 분포 를 갖는 두 개의 독립 랜덤 변수다.
f ( x ) = 2 − 2 x 을 위해 0 ≤ x < 1 F ( x ) = 2 x − x 2 을 위해 0 ≤ x < 1 E ( X ) = 1 3 VAR ( X ) = 1 18 {\displaystyle {\begin{aligned}f(x)&=2-2x{\text{ for }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ for }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}} 대칭 삼각형 분포 대칭적인 경우는 c = (a + b ) / 2. 이 경우 분포 함수의 대체 형태는 다음과 같다.
f ( x ) = ( b − c ) − c − x ( b − c ) 2 {\displaystyle {\party}f(x)&={\frac {(b-c)-c-x}{{(b-c)^{2}}\\[6pt]\end{arged}}}}}}}} 두 표준 균일 변수의 평균 분포 a = 0, b = 1 및 c = 0.5—모드(즉, 피크)는 정확히 구간의 중간에 있다. 즉, X = (X1 2 + X) / 2의 분포와 일치한다. 여기서 X 1 , X 는2 [0, 1][1] 균일 분포 를 갖는 두 개의 독립 랜덤 변수다.
f ( x ) = { 4 x 을 위해 0 ≤ x < 1 2 4 ( 1 − x ) 을 위해 1 2 ≤ x ≤ 1 {\displaystyle f(x)={\case}}{}}}}}}}{}0\leq x<{1}{1}{1}\frac{1}\4(x)&}}{{\frac{1}{1}{1}}\frac x\leq 1\case{}}}}}}}}} F ( x ) = { 2 x 2 을 위해 0 ≤ x < 1 2 2 x 2 − ( 2 x − 1 ) 2 을 위해 1 2 ≤ x ≤ 1 {\displaystyle F(x)={\begin{case}2x^{2}&{\text{{}}{{\frac{1}{1}{2}}\\x^{2}-(2x-1)^{2}&{}}}}}{\frac {1}{1}\leq 1\case{}}}}}}}}}}}}}}}}}}}}}의 경우 E ( X ) = 1 2 VAR ( X ) = 1 24 {\displaystyle {\begin}E(X)&={\frac {1}{1}{2}}\\[6pt]\operatorname {Var}(X)&={\frac {1}{24}}\end{aigned}}}}}}}} 삼각형 분산 랜덤 변수 생성 구간(0, 1)의 균등 분포 에서 무작위 변수 U를 추출한 다음 변수
X = { a + U ( b − a ) ( c − a ) 을 위해 0 < U < F ( c ) b − ( 1 − U ) ( b − a ) ( b − c ) 을 위해 F ( c ) ≤ U < 1 {\displaystyle X={\begin{cases}a+{\sqrt {U(b-a)(c-a)}}&{\text{ for }}0<U<F(c)\\&\\b-{\sqrt {(1-U)(b-a)(b-c)}}&{\text{ for }}F(c)\leq U<1\end{cases}}} [2] 여기서 F( c c a b a {\displaystyle F(c)=(c-a)/(b-a)} ( b {\displaystyle a,b} c {\displaystyle } . 이는 누적분포함수를 통해 얻을 수 있다.
분포의 사용 삼각형 분포는 일반적으로 표본 데이터가 제한적인 모집단에 대한 주관적 설명으로 사용되며, 특히 변수 사이의 관계를 알 수 있지만 데이터가 부족한 경우(아마도 수집 비용이 높기 때문일 것이다)에 사용된다. 그것은 모달 값에 대한 최소 및 최대 지식 및 "초기적인 추측"[3] 이러한 이유로 삼각형 분포는 "지식 부족" 분포라고 불려왔다.
비즈니스 시뮬레이션 따라서 삼각형 분포는 사업 의사결정 , 특히 시뮬레이션에서 자주 사용된다. 일반적으로 결과의 분포 에 대해 잘 알려지지 않은 경우(예: 가장 작고 가장 큰 값만), 균일한 분포 를 사용할 수 있다. 그러나 가장 가능성이 높은 결과가 알려지면 삼각형 분포로 결과를 시뮬레이션할 수 있다. 예 를 들어 기업 금융 에서 확인하십시오.
프로젝트 관리 삼각형 분포는 PERT 분포와 함께 프로젝트 관리(PERT 및 따라서 임계 경로 방법 (CPM)에 대한 입력으로서 최소값과 최대값으로 정의된 간격 내에 발생하는 이벤트를 모델링하는 데에도 널리 사용된다.
오디오 디더링 대칭 삼각형 분포는 일반적으로 오디오 디더링 에 사용되는데, 여기서 TPDF(삼각형 확률밀도함수)라고 한다.
빔포밍 삼각형 분포는 빔포밍과 패턴 합성에 응용된다.[4] & [5]
참고 항목 사다리꼴 분포 토머스 심슨 삼점 추정 5자리 요약 7자리 요약 삼각함수 중심 한계 정리 — 삼각형 분포는 종종 두 개의 균일한 랜덤 변수를 함께 추가한 결과로 발생한다. 즉, 삼각형 분포는 중심 한계 정리 종합 프로세스의 첫 번째 반복의 결과(항상 그렇지는 않음)인 경우가 많다(즉, n {\textstyle n=2}). 이런 의미에서 삼각분포는 때때로 자연적으로 발생할 수 있다. 더 많은 무작위 변수를 종합하는 이 과정이 계속된다면(즉 3 textstyle n\geq }), 어윈-홀 분포 — 어윈-홀 분포를 사용하는 것은 삼각 분포를 생성하는 쉬운 방법이다.베이츠 분포 - 어윈-홀 분포와 유사하지만 값이 0-1 범위로 다시 조정됨. 0 ~ 1 범위를 벗어나는 다른 삼각형 분포를 생성하기 위해 후속적으로 크기를 조정하고 이동할 수 있는 삼각형 분포를 계산하는 데 유용하다. 참조 ^ 베타 버전 이상: 한정된 지원 및 응용프로그램을 사용 하는 기타 연속적인 분포 패밀리 . 새뮤얼 코츠와 요한 레네 반 도프. https://books.google.de/books?id=JO7ICgAAQBAJ&lpg=PA1&dq=chapter%201%20dig%20out%20suitable%20substitutes%20of%20the%20beta%20distribution%20one%20of%20our%20goals&pg=PA3#v=onepage&q&f=false ^ "Archived copy" (PDF) . www.asianscientist.com . Archived from the original (PDF) on 7 April 2014. Retrieved 12 January 2022 .CS1 maint: 제목으로 보관된 복사본(링크 ) ^ "Archived copy" (PDF) . Archived from the original (PDF) on 2006-09-23. Retrieved 2006-09-23 .CS1 maint: 제목으로 보관된 복사본(링크 ) ^ Ma, Nam Nicholas; Buchanan, Kristopher; Jensen, Jeffrey; Huff, Gregory (2015). "Distributed beamforming from triangular planar random antenna arrays" . MILCOM 2015 - 2015 IEEE Military Communications Conference . pp. 553–558. doi :10.1109/MILCOM.2015.7357501 . ISBN 978-1-5090-0073-9 S2CID 3027268 . ^ K. 부캐넌, C. 플로레스 몰리나, S. 휠랜드, D. 오버서프 및 T. "분산 어레이에 적용된 바비넷의 원리," 2020 국제 응용 전자자기학회 심포지엄(ACES), 2020, 페이지 1-2, doi: 10.23919/ACES49320.2020.9196157. 외부 링크
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들





![\begin{cases}
0 & \text{for } x < a, \\
\frac{2(x-a)}{(b-a)(c-a)} & \text{for } a \le x < c, \\[4pt]
\frac{2}{b-a} & \text{for } x = c, \\[4pt]
\frac{2(b-x)}{(b-a)(b-c)} & \text{for } c < x \le b, \\[4pt]
0 & \text{for } b < x.
\end{cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e4e98ad8069ea39f61fe2f0be5b83b47f631bc)
![\begin{cases}
0 & \text{for } x \leq a, \\[2pt]
\frac{(x-a)^2}{(b-a)(c-a)} & \text{for } a < x \leq c, \\[4pt]
1-\frac{(b-x)^2}{(b-a)(b-c)} & \text{for } c < x < b, \\[4pt]
1 & \text{for } b \leq x.
\end{cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b472d4e58e4df0814805aab0a2e752d6bdebf3)

![{\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fe21e5d8eb394b9e5dca33a2c790c001328393)







![{\displaystyle \left.{\begin{array}{rl}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{array}}\right\}{\text{ for }}0\leq x\leq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d433a37e696e6f17c1e3b3baff715a391963e80d)
![{\displaystyle {\begin{aligned}\operatorname {E} (X)&={\frac {2}{3}}\\[8pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17f24b03334eae3cdacab78cc232afda9537732d)
![{\displaystyle {\begin{aligned}f(x)&=2-2x{\text{ for }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ for }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe08f03f7fa58adc4c3ff145380cf294a0ce27f7)
![{\displaystyle {\begin{aligned}f(x)&={\frac {(b-c)-|c-x|}{(b-c)^{2}}}\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9077a2e93f6ac589fc6b1b8ee5daf648a4675717)


![{\begin{aligned}E(X)&={\frac {1}{2}}\\[6pt]\operatorname {Var}(X)&={\frac {1}{24}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f5209e0fb7c8e67495e515b68623b00b681a2c)








