비중앙 t-분포

논센트럴 학생 t

확률밀도함수
매개변수	ν > 자유도 0도 ${\displaystyle ㎕\in }$ ∈ $displaystyle \mu \in \Re \,\!}$ 파라미터
지원	$(-\displaystyle x\in (-\in-\in)+\inflat )\,\!}$
PDF	본문을 보다
CDF	본문을 보다
평균	본문을 보다
모드	본문을 보다
분산	본문을 보다
왜도	본문을 보다
엑스트라 쿠르토시스	본문을 보다

비중심 t-분포는 비중심 매개변수를 사용하여 학생의 t-분포를 일반화한다.중앙 확률 분포는 시험 차이가 null일 때 검정 통계 t가 어떻게 분포되는지를 설명하는 반면, 중심 분포는 null이 거짓일 때 t가 어떻게 분포되는지를 설명한다.이것은 통계에서, 특히 통계적 힘을 계산하는 데 그 사용을 이끈다.비중심 t-분포는 단독 중심 t-분포라고도 하며, 통계적 추론에서 일차적으로 사용하는 것 외에 데이터에 대한 강력한 모델링에도 사용된다.null

정의들

Z가 단위 분산과 평균이 0인 정규 분포 랜덤 변수이고, V가 Z와 독립된 자유도가 ∆인 카이 제곱 분산 랜덤 변수라면,

${\displaystyle T={\frac {Z+\mu }{\sqrt{V/\nu }}}}}}}$

자유도와 비중심성 매개변수 μ μ 0을 갖는 비중심 t-분산 랜덤 변수. 비중심성 매개변수가 음수일 수 있다는 점에 유의한다.null

누적분포함수

자유도와 비중심성 매개변수 μ를 갖는 비중심 t-분포의 누적분포함수는 다음과^[1] 같이 표현할 수 있다.

${\displaystyle F_{\nu ,\mu }(x)={\begin{cases}{\tilde {F}}_{\nu ,\mu }(x),&{\mbox{if }}x\geq 0;\\1-{\tilde {F}}_{\nu ,-\mu }(x),&{\mbox{if }}x<0,\end{cases}}}$

어디에

${\displaystyle {\tilde{F}_{\nu,\mu }(x)=\Phi(-\mu )+{\frac {1}{1}:{2}}\sum _{j=0}^{\inflt }\왼쪽[p_{j}}I_{y}\왼쪽(j+{\frac {1}{1}:{2}},{\frac {\nu }{2}}\오른쪽)+q_{j}I_{y}\왼쪽(j+1,{\frac {\nu }{2}}\오른쪽)\오른쪽],}$

${\displaystyle I_{}}$ ${\displaystyle y_{}}$ ${\displaystyle (,}$ ${\displaystyle b}$) ${\displaystyle I_{y}\,\!(a,b)}$은(는) 정규화된 불완전한 베타 함수,

${\displaystyle y={\frac {x^{2}}:{x^{2}+\nu }},}$

${\displaystyle p_{j}={\frac {1}{j!}}}\exp \left\{-{\frac {\mu ^{2}}\{2}}\오른쪽\}\frac {\mu ^{2}}\오른쪽)^{j}}$

${\displaystyle q_{j}={\frac {\mu }{{\sqrt{2}}\감마(j+3/2)}}}\exp \left\{-{\frac {\mu ^{2}}\{2}}\오른쪽\}\frac {\mu ^{2}}\오른쪽)^{j}}$

φ은 표준 정규 분포의 누적 분포 함수다.null

또는 중심 t-분포 CDF는 다음과 같이^{[citation needed]} 표현할 수 있다.

${\displaystyle F_{v,\mu }(x)={\begin{case}{1}{1}{1}:{1}:{\frac {1}{2}}\sum _{j=0}^{\inflt }{\frac {1}{j!}}}}(-\mu {2}})^{j}e^{\frac {-\mu ^{2}}:{{2}}:{\frac {\j+1}{2}}:{\frac {\j+1}}}{\sqrt {\pi }}}}}}}I\왼쪽({\frac {v}{v+x^{2)}}};{\frac {v}{2}},{\frac {j+1}{2}}\\오른쪽),&x\geq 0\\\1-{\frac {1}2}}\sum _{j=0}^{\frac {1}{j!}}}}(-\mu {2}})^{j}e^{\frac {-\mu ^{2}}:{{2}}:{\frac {\j+1}{2}}:{\frac {\j+1}}}{\sqrt {\pi }}}}}}}I\왼쪽({\frac {v}{v+x^{2)}}};{\frac {v}{2}},{\frac {j+1}{2}}\오른쪽),&x<0\end{case}}}}$

여기서 γ은 감마함수이고 나는 정규화된 불완전 베타함수다.null

누적분포함수의 다른 형태도 있지만, 위에 제시된 첫 번째 형태는 재귀적 컴퓨팅을 통해 평가하기가 매우 쉽다.^[1]통계 소프트웨어 R에서는 누적분포함수를 pt로 구현한다.null

확률밀도함수

자유도가 0도 이하인 비중심 t-분포에 대한 확률밀도함수(pdf)와 비중심성 매개변수 μ는 여러 형태로 표현할 수 있다.null

밀도함수의 결합초기하함수 형태는

${\displaystyle f(x)=\underbrace {{\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-{\tfrac {\nu +1}{2}}}} _{{\text{StudentT}}}(x\,;\,\mu =0)\exp {\big (}-{\tfrac {\mu ^{2}}:{\big )}{\Big \{}A_{\nu }(x\,;\,\mu )+B_{\nu }(x\,;\,\mu ){\Big \},}$

어디에

${\displaystyle {\reasoned}A_{\nu }(x\,;\,\mu )&={_{1}F}_{1}\left({\frac {\nu +1}{2}}\,;\,{\frac {1}{2}}\,;\,{\frac {\mu ^{2}x^{2}}{2(x^{2}+\nu )}}\right),\\B_{\nu }(x\,;\,\mu )&={\frac {{\sqrt {2}}\mu x}{\sqrt {x^{2}+\nu }}}{\frac {\Gamma ({\frac {\nu }{2}}+1)}{\감마({\frac {\nu +1}{2}})}{_{1}}F}_{1}\왼쪽({\frac {\nu }{2}}+1\,;\,{\frac {3}{2}}:\,;\,\,\\\frac {\mu ^{2}x^{2}}:{2}(x^{2}+\오른쪽),\end{aigned}}}}}}}}}}}}}$

여기서 F는₁ 결합초기하함수다.null

대체적으로 통합된 형태는^[2]

${\displaystyle f(x)={\frac {\nu ^{\frac {\nu }}:{2}}: exp \frac{\nu \frac{\nu ^{2}}(x^{2}+\nu )}\오른쪽)}{{\sqrt {\pi }}\Gamma ({\frac {\nu }{2}})2^{\frac {\nu -1}{2}}(x^{2}+\nu )^{\frac {\nu +1}{2}}}}\int _{0}^{\infty }y^{\nu }\exp \left(-{\frac {1}{2}}\left(y-{\frac {\mu x}{\sqrt {x^{2}+\nu }}}\right)^{2}\right)dy.}$

세 번째 형태의 밀도는 다음과 같이 누적분포함수를 사용하여 얻는다.null

${\displaystyle f(x)={\preas}{\frac {\nu }{x}}\왼쪽\{{{}}F_{\nu +2,\mu }\left(x{\sqrt {1+{\frac {2}{\nu }}}}\right)-F_{\nu ,\mu }(x)\right\},&{\mbox{if }}x\neq 0;\\{\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\pi \nu }}\Gamma ({\frac {\nu }{2}})}}\exp \left(-{\frac {\mu ^{2}}{2}}\right),&{\mbox{if }}x=0.\end{case}}}$

이것은 R에서 dt 함수에 의해 구현된 접근법이다.

특성.

중심 t-분포의 모멘트

일반적으로 비중앙 t-분포의 k번째 원시 모멘트는^[3]

${\displaystyle {\mbox{E}\왼쪽[]T^{k}\right]=ᆮ\left({\frac{\nu}{2}}\right)^{\frac{k}{2}}{\frac{\Gamma)}{\Gamma \left({\frac{\nu}{2}}\right)}}{\mbox{exp}}\left(-{\frac{\mu ^{2}}{2}}\right){\frac{d^{k}}{d\mu ^{km그리고 4.9초 만}}}{\mbox{exp}}\left({\frac{\mu ^{2}}{2}}\right),&,{\mbox{만약}}\nu>k, \\{\mbox{존재하지 않나}},&,{\mbox{만약}}.\nu \leq k.\\end{case}}$

특히 비중앙 t-분포의 평균과 분산은 다음과 같다.

${\displaystyle {\begin{aigned}{\mbox{E}\왼쪽[]T\right]&={\begin{cases}\mu {\sqrt {\frac {\nu }{2}}}{\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}},&{\mbox{if }}\nu >1;\\{\mbox{Does not exist}},&{\mbox{if }}\nu \leq 1,\\\end{cases}}\\{\mbox{Var}}\left[T\right]&={\begin{cases}{\frac {\nu (1+\mu ^{2})}{\nu -2}}-{\frac {\mu ^{2}\nu }{2}}\left({\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}\right)^{2},&{\mbox{if }}\nu >2;\\{\mbox{Does not exist}},&{\mbox{if }}\nu \leq 2.\\end{case}\end{aigned}}}$

An excellent approximation to ${\displaystyle {\sqrt {\frac {\nu }{2}}}{\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}}$ is ${\displaystyle \left(1-{\frac {3}{4\nu -1}}\right)^{-1}}$, which can be used in both formulas.null

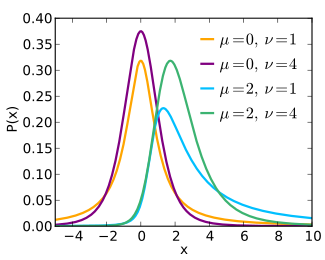
비대칭

중심 t-분포는 μ가 0, 즉 중심 t-분포가 아닌 한 비대칭이다.또한, 비대칭성은 자유도가 클수록 작아진다.오른쪽 꼬리는 μ가 0일 때 왼쪽보다 무겁고, 반대로 μ가 0일 때 오른쪽 꼬리는 μ가 0일 때 왼쪽보다 무거울 것이다.그러나 보통 왜도는 일반적으로 이 분포에 대한 좋은 비대칭 척도가 아니다. 자유도가 3보다 크지 않으면 세 번째 순간이 전혀 존재하지 않기 때문이다.자유도가 3보다 크더라도 표본 크기가 매우 크지 않은 한 왜도의 표본 추정치는 여전히 매우 불안정하다.null

모드

비중앙 t-분포는 항상 단조롭고 종 모양이지만, μ μ 0의 경우에는 분석적으로^[4] 사용할 수 없다.

${\displaystyle {\sqrt {\frac {\nu}{\nu + (5/2)}}{\frac {\mathrm {mod}{\mu }}{\frac {}{\nu +1}}}}}}}}{\frac {\nu +1}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

특히 모드는 항상 비중심성 파라미터 μ와 동일한 부호를 가진다.더욱이 이 모드의 음은 정확히 자유도는 같지만 비중심성 매개변수 -μ를 갖는 비중심 t-분포에 대한 모드다.null

모드는 μ와 함께 엄격히 증가하고 있다(항상 μ가 조정되는 방향과 같은 방향으로 이동한다).한계에서 μ → 0일 때 모드는 다음과 같이 근사치된다.

${\displaystyle {\sqrt {\frac {\nu }{2}}:}{\frac {\nu +2}{2}}:\오른쪽){\Gamma \left({\frac {\nu +3}{2}}\오른쪽)}}}{\ma;},}$

그리고 μ → μs일 때 모드는 다음과 같이 근사치된다.

${\displaystyle {\sqrt {\frac {\nu}{\nu +1}}\mu.}$

관련 분포

• 중심 t-분포: 중심 t-분포를 위치/척도 패밀리로 변환할 수 있다.이 분포군은 다양한 꼬리 행동을 포착하기 위해 데이터 모델링에 사용된다.중심 t-분포의 위치/규모 일반화는 이 글에서 논한 중심 t-분포와는 다른 분포다.특히 이 근사치는 중심 t-분포의 비대칭성을 존중하지 않는다.단, 중심 t-분포는 비중심 t-분포에 대한 근사치로 사용할 수 있다.^[5]
• T가 자유도와 비중심도 매개변수 μ와 F = T로² 비중심 t-분포된 경우, F는 자유도가 1분자, 자유도가 μ인² 비중심 F-분포를 가진다.
• T가 자유도와 비중심성 매개변수 μ와 함께 중심 t-분산되지 않은 경우${\displaystyle ,}$ 그리고 $Z{\displaystyle }$ = ${\displaystyle \underset{}{lim}}$ ${\displaystyle \underset{}{}\underset{}{}}$→ ${\displaystyle \underset{}{\mathrm{\infty }}}$ T ${\displaystyle Z=\lim _{\nu \rightarrow \inft }T$ 평균 μ와 단위 분산을 갖는 정규 분포를 가진다.
• 이중 중심 t-분포의 분모 비중심성 매개변수가 0이면 비중심 t-분포가 된다.

특례

• μ = 0일 때, 비중앙 t 분포는 같은 자유도의 중앙(학생) t 분포가 된다.

발생 및 적용

전력 분석에 사용

우리가 독립적이고 동일한 분포의 표본 X₁, ..., X를_n 가지고 있다고 가정하자. 각각은 평균 θ과 분산 σ으로² 분포하며, 귀무 가설 hypothesis = 0 대 대립 가설 hypothesis 0을 검정하는 데 관심이 있다.테스트 통계를 사용하여 하나의 샘플 t-검정을 수행할 수 있다.

${\displaystyle T={\frac {\bar {X}}{{\hat {\sigma }}/{\sqrt {n}}}}={\frac {{\frac {{\bar {X}}-\theta }{(\sigma /{\sqrt {n}})}}+{\frac {\theta }{(\sigma /{\sqrt {n}})}}}{\sqrt {\left.\left \frac {{\hat{\\\chatma }}:{2}}:{\nma ^{2}/(n-1)}\right/(n-1)}}}}}}}}}}}}}}$

여기서 $X$의$${\$displaystyle {\bar {X}$은(는) 표본 평균이고 ^${\displaystyle {}^{}}{\displaystyle {\stackrel{}{^}}^{}}$ ${\displaystyle 2^{\mathrm{}}}$ {\$displaystyle {\hat$ {\$sigma }}}{2}\,\}$은(는) 편향되지 않은 표본 분산이다.두 번째 등등의 오른손은 위에서 설명한 비중심 t 분포의 특성화와 정확히 일치하므로, T는 자유도가 n-1도인 비중심 t 분포와 비중심적 매개변수 $n{\displaystyle \sqrt{}}$ ${\displaystyle \theta }$/${\displaystyle \sigma }$ $sqrt {\n}\$sqrt ${\n}\sigma \,\}$을(를) 가지고 있다$.$

그(중앙)T분포의 이 시험의 힘giv은pre-specified α ∈(0,1), 때마다 T>만약 시험 절차는 1− α는 공 가설을 거부한다면/2{\displaystyle T>t_{1-\alpha /2}\,\!}, t1− α/2{\displaystyle t_{1-\alpha /2}\,\!}을 상단 α/2 분위수.부러움

${\displaystyle 1-F_{n-1,{\sqrt{n}\theta /\sigma }(t_{1-\alpha /2})+F_{n-1,{\sqrt{n}\sigma }(-t_{1-\alpha /2})}$

비중심 t-분포의 유사한 용도는 위의 표본 t-검정을 특수 사례로 포함하는 일반 이론 선형 모델의 검정력 분석에서 확인할 수 있다.null

공차 구간에서 사용

단측 정규 공차 구간은 중심 t-분포에 기초한 표본 평균 및 표본 분산 측면에서 정확한 해법이 있다.^[6]이를 통해 표본 모집단의 특정 비율이 어느 정도 신뢰 수준에서 포함되는 통계적 간격을 계산할 수 있다.null

참고 항목

• 비중앙 F-분포

참조

외부 링크

• 에릭 W. 와이스슈타인 "비중앙학생 t-Distribution."From MathWorld—Wolfram 웹 리소스
• 생명 또는 과학에 대한 높은 정확도 계산: Casio 회사의 noncentral t-distribution.