어윈-홀 분포

어윈-홀 분포

확률밀도함수
누적분포함수
매개변수	n ∈ N0
지원	$[0,n]에서 [\displaystyle x\in]$
PDF	${\displaystyle {\frac {1}{(n-1)!}}}}\sum _{k=0}^{\lfloor x(-1)^{{k}{\binom{n}}{k}(x-k)^{n-1}$
CDF	${\displaystyle {\frac {1}{n!}}}\sum _{k=0}^{\lfloor x(-1)^{{k}{\binom {n}{k}}(x-k)^{n}}}}}}}}}$
평균	${\displaystyle {\frac{n}{2}}:}$
중앙값	${\displaystyle {\frac{n}{2}}:}$
모드	${\displaystyle{\case}{\text{case}{{}}}}}{0,1]&{\text{}}{\frac{n}{2}}&{\text}\end{case}}}}}}의 모든 값$
분산	${\displaystyle {\frac{n}{12}}}$
왜도	0
엑스트라 쿠르토시스	${\displaystyle -{\tfrac {6}{5n}}$
MGF	${\displaystyle {\left\\frac {\mathrm {e}^{t}-1}{t}\오른쪽)^{n}}}}}}}:{n}}$
CF	${\displaystyle {\좌측값\frac {\mathrm {e}^{it}-1}{it}\우측)^{n}}}}}}}}}}$

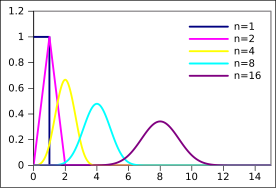
확률과 통계에서, 조셉 오스카 어윈과 필립 홀의 이름을 딴 어윈-홀 분포는 다수의 독립 랜덤 변수의 합으로 정의된 랜덤 변수에 대한 확률 분포로, 각각 균일한 분포를 가진다.^[1] 이러한 이유로 균일한 합계 분포로도 알려져 있다.

대략적으로 정규 분포를 갖는 의사 난수의 생성은 대개 프로그래밍의 단순성을 위해 균일한 분포를 갖는 의사 난수의 합계를 계산하여 이루어지기도 한다. 어윈-홀 분포를 재조정하면 생성되는 랜덤 변수의 정확한 분포를 제공한다.

이 분포는 때때로 0에서 1까지 균일하게 분포된 n개의 독립 랜덤 변수의 평균(합이 아님)인 Bates 분포와 혼동되기도 한다.

정의

Irwin-Hall 분포는 n개의 독립적이고 동일한 분포의 U(0, 1) 랜덤 변수의 합에 대한 연속 확률 분포다.

${\displaystyle X=\sum _{k=1}^{n}U_{k}.}$

확률밀도함수(pdf)는 다음과 같이 주어진다.

${\displaystyle f_{X}(x;n)={\frac {1}{2(n-1)!}}}\sum _{k=0}^{n(1)^{k}{n \선택 k}(x-k)^{n-1}\sgnname {sgn}(x-k)}$

여기서 sgn(x - k)은 부호 함수를 나타낸다.

${\displaystyle \sgn}(x-k)={\display{case}-1&x<0&x=k\1&x}k.\end{case}}}$

따라서 pdf는 매듭 0, 1, ..., n에 걸쳐 n - 1의 스플라인(부분 다항식 함수)이다. 실제로 k와 k + 1에 위치한 매듭 사이의 x의 경우 pdf는 다음과 같다.

${\displaystyle f_{X}(x;n)={\frac {1}{(n-1)!}}}\sum _{j=0}^{n-1a_{j}(k,n)x^{j}}}$

k에 대한 반복 관계에서 계수 a(k,n)를_j 찾을 수 있는 경우

${\displaystyle a_{j}(k,n)={\begin{cases}1&k=0,j=n-1\\0&k=0,j<n-1\\a_{j}(k-1,n)+(-1)^{n+k-j-1}{n \choose k}{{n-1} \choose j}k^{n-j-1}&k>0\end{cases}}}$

계수는 OEIS에서도 A188816이다. 누적분포의 계수는 A188668이다.

평균과 분산은 각각 n/2와 n/12이다.

특례

• n = 1의 경우 X는 균일한 분포를 따른다.

${\displaystyle f_{X}(x)={\begin{case}1&0\leq x\leq 1\\\0&{\text}{otherwise}\case}}}}$

• n = 2의 경우 X는 삼각형 분포를 따른다.

${\displaystyle f_{X}(x)={\begin}x&0\leq x\leq 1\\2-x&1\leq x\leq 2\end{case}}}}$

• n = 3의 경우,

${\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{2}}x^{2}&0\leq x\leq 1\\{\frac {1}{2}}(-2x^{2}+6x-3)&1\leq x\leq 2\\{\frac {1}{2}}(3-x)^{2}&2\leq x\leq 3\end{cases}}}$

• n = 4의 경우,

${\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{6}}x^{3}&0\leq x\leq 1\\{\frac {1}{6}}(-3x^{3}+12x^{2}-12x+4)&1\leq x\leq 2\\{\frac {1}{6}}(3x^{3}-24x^{2}+60x-44)&2\leq x\leq 3\\{\frac {1}{6}}(4-x)^{3}&3\leq x\leq 4\end{cases}}}$

• n = 5의 경우,

${\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{24}}x^{4}&0\leq x\leq 1\\{\frac {1}{24}}(-4x^{4}+20x^{3}-30x^{2}+20x-5)&1\leq x\leq 2\\{\frac {1}{24}}(6x^{4}-60x^{3}+210x^{2}-300x+155)&2\leq x\leq 3\\{\frac {1}{24}}(-4x^{4}+60x^{3}-330x^{2}+780x-655)&3\leq x\leq 4\\{\frac {1}{24}}(5-x)^{4}&4\leq x\leq 5\end{cases}}}$

정규 분포 근사치

By the Central Limit Theorem, as n increases, the Irwin-Hall distribution more and more strongly approximates a Normal distribution with mean ${\displaystyle \mu =n/2}$ and variance ${\displaystyle \sigma ^{2}=n/12}$. To approximate the standard Normal distribution ${\displaystyle \varphi (x)=\mathcal{N}(\mu =0,{\sigma }^2=1}$${\displaystyle )}$ ${\displaystyle \phi (x)={\mathcal{N}}(\mu =0,\sigma$^{$2}=1$ Irwin-Hall 분포는 n/2의 평균으로 이동하고 분산에 대한 반제곱근으로 결과를 확장하여 중심을 잡을 수 있다.

${\displaystyle \phi(x)\traft {12/n}\reft(f_{X}(x;n)-n/2)\right)_{n\g:1}}$

이러한 파생은 제곱근을 제거하는 계산적으로 간단한 경험적 발견으로 이어지며, 표준 정규 분포를 12개의 균일한 U(0,1)의 합으로 근사하게 추정할 수 있다.

${\displaystyle \phi(x)\trawth f_{X}(x;12)-6=\sum _{k=1}^{12}U_{k}-6}$

유사 및 관련 분포

어윈-홀 분포는 베이츠 분포와 유사하지만 여전히 정수만 매개변수로 나타낸다. N - 트렁크(N)를 너비로 하여 랜덤 균일 변수까지 추가하면 실제 값 매개변수에 대한 확장이 가능하다.

어윈-홀 분포 확장

데이터 적합 목적으로 Irwin-Hall을 사용할 때 한 가지 문제는 매개변수 n이 정수여야 하기 때문에 IH가 매우 유연하지 않다는 것이다. 그러나 동일한 균일 분포를 합하는 대신 예를 들면 다음과 같이 추가할 수 있다. U + 0.5또한 사례 n = 1.5(사다리꼴 분포 제공)를 다루는 U.

어윈-홀 분포는 참고문헌의 그림 1에서 빔포밍과 패턴 합성을 위한 애플리케이션을 가지고 있다.

참고 항목

• 베이츠 분포
• 정규 분포
• 중앙 한계 정리
• 균일 분포(연속)
• 삼각분포

메모들

참조

• Hall, Philip. (1927) "변수가 0과 1 사이의 값을 갖는 모집단에서 추출한 N 크기의 표본에 대한 평균 분포, 모든 그러한 값은 동등하게 개연성이 있다." 바이오메트리카, 제19권, 제3/4호, 페이지 240–245. 도이:10.1093/바이오메트/19.3-4.240 JSTOR 2331961
• 어윈, J.O. (1927년) "유한 모멘트를 갖는 빈도수 법칙을 가진 모집단에서 추출한 표본의 빈도 분포에 관하여, Pearson의 유형 II를 특별히 참조한다." 바이오메트리카, 제19권, 제3/4호, 페이지 225–239. 도이:10.1093/바이오메트/19.3-4.25 JSTOR 2331960