역가우스 분포

역가우스어

확률밀도함수
누적분포함수
표기법	${\displaystyle \vmsname {IG} \left(\mu ,\lambda \right)}$
매개변수	$\displaystyle \mu >0}$ $\displaystyle \lambda >0}$
지원	$(0,\displaystyle x\in (0,\fty )}$
PDF	${\displaystyle {\sqrt {\frac {\pi x^{3}}}\ex \exe \좌측[-{\fracta {\fracta (x-\mu )^{2}}:{2\mu ^{2}x}\오른쪽]}}$
CDF	${\displaystyle \Phi \left({\sqrt {\frac {\lambda }}}}{\frac {x}{\mu }-1\오른쪽)}}$ ${\displaystyle {}+\exp \left\frac {2\fractda }{\mu }}\오른쪽)\Phi \left(-{\sqrt {\frac {\lambda }}}}{x}\좌({\frac {x}{\mu }+1\우)\우)}$ 여기서 $\phi {\displaystyle \mathrm{}}$ ${\displaystyle \Phi }$은(는) 표준 정규(표준 가우스) 분포 c.d.f이다.
평균	${\displaystyle \operatorname {E} [X]=\mu }$ ${\displaystyle \operatorname {E} [{\frac {1}{X}}]={\frac {1}{\mu }+{\frac {1}{\lambda }}}}}}$
모드	${\displaystyle \mu \left[1+{\frac {9\mu ^{2}}:{2}}:}\frac {1}{1}:{1}{{1}-{3\mu }{2\mu }}}\right]}}$
분산	${\displaystyle \operatorname {Var} [X]={\frac {\mu ^{3}{\lambda }}}$ ${\displaystyle \operatorname {Var} [{\frac {1}{X}}]={\frac {1}{\mu \lambda }}+{\frac {2}{\lambda ^{2}}:}$
왜도	${\displaystyle 3\왼쪽 사진\frac {\mu }{\buffda }}\오른쪽)^{1/2}}$
엑스트라 쿠르토시스	${\displaystyle {\frac {15\mu }{\buffda }}}$
MGF	${\displaystyle \exp \left[{\frac{\black}{1-{\sqrt{1-{\frac{2\mu ^{2}t}{\nota }}}}\right]}}}$
CF	${\displaystyle \exp \left[{\frac{\prox{1-{\sqrt{1-{\frac{2\mu ^{2}\mathrm {i}{\proda }}}}\right]}}}}}$

확률론에서 역가우스 분포(Wald 분포라고도 함)는 (0,920)를 지지하는 연속 확률 분포의 2-모수 계열이다.null

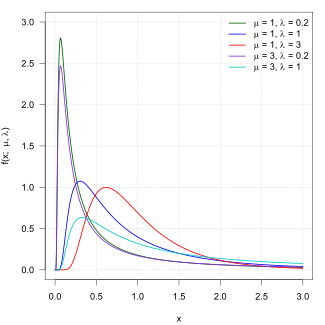
확률밀도함수는 다음과 같다.

${\displaystyle f(x;\mu ,\bigda )={\sqrt {}{{2\pi x^{3}}}}\exp {\biggl (}-{{\frac {\biggl)(}-{\frac {\mu )^{2\x}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}*$

x > 0의 경우, 여기서 > ${\displaystyle \mu >0}$은 평균이고 > 0${\displaystyle$\ \$da >0}$은 형상 매개변수다.^[1]null

역 가우스 분포는 가우스 분포와 유사한 여러 특성을 가지고 있다.이름은 오해의 소지가 있을 수 있는데, 가우스안은 정해진 시간에 브라운 운동 레벨을 기술하는 반면, 역 가우스안은 긍정적인 표류를 가진 브라운 운동이 고정된 양수 수준에 도달하는 시간의 분포를 기술한다.null

누적 생성 함수(특성 함수의 로그)는 가우스 랜덤 변수의 누적 생성 함수의 역이다.null

$랜덤{\displaystyle }$ 변수 X가 평균 μ와 형상 파라미터 parameter으로 가우스 분포를 역분산한다는 것을 나타내기 위해 X${\displaystyle }$~ ${\displaystyle \mathrm{IG}}$ ${\displaystyle }$ ${\displaystyle (\mu }$ , ${\displaystyle ,}$ $displaystyle X\sim \operatorname {IG}(\mu ,\lambda )\,\}$을$(!\}).$

특성.

단일 매개변수 양식

역가우스 분포의 확률밀도함수(pdf)는 다음과 같은 단일 매개변수 형태를 가진다.

${\displaystyle f(x;\mu ,\mu ^{2})={\frac {2\pi x^{3}}}\exp {\biggl (}-{{\frac {(x-\mu )^{2x}{\biggr )}.}$

이 형태에서 분포의 ${\displaystyle \mathrm{평균}}$과 분산은 $E{\displaystyle \mathbb{}}$[ X ${\displaystyle ]}$= ${\displaystyle \mathrm{Var}}$( X${\displaystyle }$)${\displaystyle }$. ${\displaystyle \mathb {E}[X]={\text{Var}(X$)이다$.$$}$

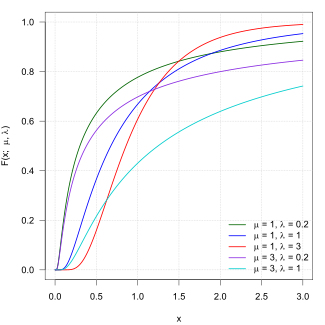
또한 단일 모수 역가우스 분포의 누적분포함수(cdf)는 다음과 같은 방법으로 표준 정규 분포와 관련이 있다.

${\displaystyle {\begin{aligned}\Pr(X<x)&=\Phi (z_{1})+e^{\mu }\Phi (z_{2}),&{\text{for}}&\quad 0<x\leq \mu ,\\\Pr(X>x)&=\Phi (-z_{1})-e^{\mu }\Phi (z_{2}),&{\text{for}}&\quad x\geq \mu .\end{aligned}}}$

where ${\displaystyle z_{1}={\frac {\mu }{x^{1/2}}}-x^{1/2}}$ and ${\displaystyle z_{2}={\frac {\mu }{x^{1/2}}}+x^{1/2},}$ where the ${\displaystyle \Phi }$ is the cdf of standard normal distribution.변수 $z{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ ${\displaystyle z_{}}$ $2{\displaystyle {}_{}}$ ${\$}}은 ID $z{\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$= z ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ ${\displaystyle \mathrm{4\mu }.}$ ${\displaysty z_{2}^{2}=z_{1}^{2}+4\mu .}$에 의해 서로 연관되어$$ 있다.

단일 파라미터 양식에서 MGF는

${\displaystyle M(t)=\exp[\mu(1-{\sqrt{1-2t}).}$

An inverse Gaussian distribution in double parameter form ${\displaystyle f(x;\mu ,\lambda )}$ can be transformed into a single parameter form ${\displaystyle f(y;\mu _{0},\mu _{0}^{2})}$ by appropriate scaling ${\displaystyle y={\frac {\mu ^{2}x}{\lambda }},}$$$ 여기서 $\mu {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle {\mu \mathrm{}}^{}}$ 3${\displaystyle {}^{}}$/$$. {\$displaystyle \mu _{0}=\mu ^{3}/\muda .}$

역가우스 분포의 표준 형식은

${\displaystyle f(x;1,1)={\frac {1}{\sqrt{2\pi x^{3}}}}\exp {\biggl (}-{\frac {(x-1)^{2x}{\biggr )}.}$

합계

X에_i ${\displaystyle \mathrm{IG}}$ ${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle i_{}}$, ${\displaystyle {}_{}}$ 0 ${\displaystyle {w\mathrm{}}_{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 2${\displaystyle {}_{}^{}}$) $displaystyle \operatorname {IG}(\mu _{0}w_{i}^{2$})이$$ 있고$,$ i = 1, 2, ..., n에 대한 분포가 모두 독립된 경우, 그 다음, X에_i 대한 분포가 모두 독립된 경우,

${\displaystyle S=\sum _{i=1}^{n}X_{i}\sim \operatorname {IG} \left(\mu _{0}\sum w_{i},\lambda _{0}\left(\sum w_{i}\right)^{2}\right).}$

참고:

${\displaystyle {\frac {\operatorname {Var}(X_{i}){\operatorname {E}(X_{i})}}}={\frac{\mu _{0}^{2}w_{i}^{2}}:{\flada _{0}w_{i}^{2}}={\frac {\mu _{0}^{0}}}}{0}}:{0}}}:{0}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}:}$

모든 나에겐 일정하다.이것은 합산을 위해 필요한 조건이다.그렇지 않으면 S는 역 가우스 분포가 아닐 것이다.null

스케일링

어떤 t > 0에 대해서도 그것은 다음을 지탱한다.

${\displaystyle X\sim \operatorname {IG}(\mu ,\lambda )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\X\sim\\\\operatorname {IG}(t\mu ,t\mu ,t\\\\\\\\\\mu ,t\\\\\\\\\\\\\\\\\\\\\\\\\\\\}$

지수군

역가우스 분포는 자연적 모수 -³/(2μ²) 및 -³/2와 자연 통계 X와 1/X를 갖는 2-모수 지수 계열이다.null

브라운 운동과의 관계

확률적 공정 X는_t 다음과 같이 제공된다.

${\displaystyle X_{0}=0\quad }$

${\displaystyle X_{t}=\nu t+\sigma W_{t}\quad \quad \quad }$

여기서 W는_t 표준 브라운 운동이다.즉, X는_t 드리프트 > 0 ${\displaystyle \nu >0}$을(를) 가진 브라운 운동이다

그런 다음 X에_t 의한 고정 레벨 > 0 ${\displaystyle \alpha >0}$에 대한 첫 번째 통과 시간은 반 가우스파에 따라 분포한다.

${\displaystyle T_{\alpha }=\inf\{t}0\mid X_{t}=\alpha \}\sim \operatorname {IG} \left({\frac {\alpha }{\nu }},\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp {\biggl (}-{\frac {(\alpha -\nu x)^{2}}{2\sigma ^{2}x}}{\biggr )}}$

즉

${\displaystyle P(T_{\alpha }\in (T,T+dT))={\frac {\alpha }{\sigma {2\pi T^{3}}}\exp {\biggl (}-{{-{\frac {(\alpha -\nu T)^{2}}:{2\sigma ^{2}T}{\biggr )}dT}$

(cf. Schrödinger^[2] 방정식 19, Smoluchowski^[3], 방정식 8, Peoples^[4], 방정식 1)null

드리프트가 0일 때

위와 같은 일반적인 특별한 경우는 브라운의 운동이 표류하지 않을 때 발생한다.이 경우 매개변수 μ는 무한대 경향이 있으며, 고정 레벨 α에 대한 첫 번째 통과 시간은 확률 밀도 함수를 가진다.

${\displaystyle f\lift(x;0,\left\frac {}{\pi }}\right)={\fract{2\pi x^{3}}}}} exp \frac{2\pi ^{2}\fracma ^{2}xx}}}}}}}}}}}}}}}}}}}}}}}$

(또한 바첼리어^{[5]: 74 [6]: 39} 참조).이것은$$ $파라미터{\displaystyle }$c${\displaystyle {}^{}}$= (${\displaystyle {\alpha \frac{}{}}^{}}$ ${\displaystyle {\frac{\alpha }{}}^{}}$) ${\displaystyle {\mathrm{}}^{}}$ ${\$ $\mu {\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \mu =0$인 레비 분포다.

최대우도

모델 where

${\displaystyle X_{i}\심 \operatorname {IG}(\mu ,\lambda w_{i})\,\,\,\,\,\,i=1,2,\ldots,n}$

모든 것을 알고_i, (μ, μ)를 알 수 없고, 모든 X가_i 다음과 같은 우도 함수를 가지고 있다.

${\displaystyle L(\mu ,\lambda )=\left({\frac {\lambda }{2\pi }}\right)^{\frac {n}{2}}\left(\prod _{i=1}^{n}{\frac {w_{i}}{X_{i}^{3}}}\right)^{\frac {1}{2}}\exp \left({\frac {\lambda }{\mu }}\sum _{i=1}^{n}w_{i}-{\frac {\lambda }{2\mu ^{2}}}\sum _{i=1}^{n}w_{i}X_{i}-{\frac {\lambda }{2}}\sum _{i=1}^{n}w_{i}{\frac {1}{X_{i}}}\right).}$

우도 방정식을 풀면 다음과 같은 최대우도 추정치가 산출된다.

${\displaystyle {\widehat {\mu }}={\frac {\sum _{i=1}^{n}w_{i}X_{i}}{\sum _{i=1}^{n}w_{i}}},\,\,\,\,\,\,\,\,{\frac {1}{\widehat {\lambda }}}={\frac {1}{n}}\sum _{i=1}^{n}w_{i}\left({\frac {1}{X_{i}}}-{\frac {1}{\widehat {\mu }}}\right).}$

${\displaystyle \hat{\mu }}$ ${\$과(와) $\lambda {\displaystyle \hat{}}${\$displaystyle${\$widehat {\prowidda$}}}은(는$$) 독립적이며

${\displaystyle {\widehat {\mu}\sim \chostname {IG} \left(\mu ,\lambda \sum _{i=1}^{n1}w_{i}\right),\qquad {\frac {n}{\widehat{\lambda }}}}}\sim {\frac {1}{n-1}^{n1}{2}.}$

반가우스 분포에서 표본 추출

다음과 같은 알고리즘을 사용할 수 있다.^[7]null

평균이 0이고 표준 편차가 1인 정규 분포에서 랜덤 변수 생성

$[\displaystyle \displaystyle \nu \sim N(0,1)]}$

값을 제곱하다

${\displaystyle \displaystyle y=\nu ^{2}}$

그리고 관계를 이용한다.

${\displaystyle x=\mu +{\frac {\2}y}{2\fracda }-{{\frac {\mu}{2\dada }}}{\sqrt {4\mu \e+\mu ^{2}y^}}}}}}.}$

0과 1 사이의 균일한 분포에서 샘플링된 또 다른 랜덤 변수 생성

$[\displaystyle \displaystyle z\sim U(0,1)]}$

$z{\displaystyle \frac{\mathrm{\mu \mu \mu }}{}}$ +${\displaystyle \frac{}{}}$x ${\$mu +x}}인$경우$x {\$displaystyle \displaystyle$ x}을$(를)$ 반환하고$$ $\mu {\displaystyle \frac{{}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$ . ${\displaystystyle {\\frac$ {\mu$^{$2}}:{$x}{x}.$$}$

Java의 샘플 코드:

공중의 곱절로 하다 가우스 역(곱절로 하다 뮤, 곱절로 하다 람다) {     무작위 랜드 = 새로운 무작위();     곱절로 하다 v = 랜드.넥스트가우스어();  // 평균이 0이고 표준 편차가 1인 정규 분포로부터 표본 추출     곱절로 하다 y = v * v;     곱절로 하다 x = 뮤 + (뮤 * 뮤 * y) / (2 * 람다) - (뮤 / (2 * 람다)) * 수학.sqrt(4 * 뮤 * 람다 * y + 뮤 * 뮤 * y * y);     곱절로 하다 시험하다 = 랜드.넥스트더블();  // 0과 1 사이의 균일한 분포에서 추출한 표본     만일 (시험하다 <= (뮤) / (뮤 + x))         돌아오다 x;     다른         돌아오다 (뮤 * 뮤) / x; } 

Matplotlib 및 NumPy를 사용하여 Python을 사용한 월드 분포

그리고 매트릭리브와 NumPy를 사용하여 파이썬에서 월드 분포를 플로팅하려면:

수입하다 매플리브피플롯 로서 plt 수입하다 불결한 로서 np  h = plt.히스(np.무작위의.갈다(3, 2, 100000), 통에 담다=200, 밀도=진실의)  plt.보여 주다() 

관련 분포

• If ${\displaystyle X\sim \operatorname {IG} (\mu ,\lambda )}$, then ${\displaystyle kX\sim \operatorname {IG} (k\mu ,k\lambda )}$ for any number ${\displaystyle k>0.$$}$^[1]
• If ${\displaystyle X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,}$ then ${\displaystyle \sum _{i=1}^{n}X_{i}\sim \operatorname {IG} (n\mu ,n^{2}\lambda )\,}$
• If ${\displaystyle X_{i}\sim \operatorname {IG} (\mu ,\lambda )\,}$ for ${\displaystyle i=1,\ldots ,n\,}$ then ${\displaystyle {\bar {X}}\sim \operatorname {IG} (\mu ,n\lambda )\,}$
• If ${\displaystyle X_{i}\sim \operatorname {IG} (\mu _{i},2\mu _{i}^{2})\,}$ then ${\displaystyle \sum _{i=1}^{n}X_{i}\sim \operatorname {$$IG} \left(\sum \sum _{i=1}^{n}\mu _{i=1}\left(\sum _{i=1}^{n}\mu _{i}\right)\,}$
• If ${\displaystyle X\sim \operatorname {IG} (\mu ,\lambda )}$, then ${\displaystyle \lambda (X-\mu )^{2}/\mu ^{2}X\sim \chi ^{2}(1)}$.^[8]

역 가우스 분포(Wald 분포)와 지수 분포(전 Wald 분포)의 콘볼루션은 심리학에서 응답 시간의 모델로 사용되며,^[9] 시각적 검색이 한 예다.^[10]null

역사

이 분포는 한 주식이 처음으로 특정 가격에 도달하는 시점에 루이 바첼리에^[5][6] 의해 1900년에 처음으로 도출된 것으로 보인다.1915년 에르윈 슈뢰딩거와^[2] 마리안 대 스몰루코프스키에^[3] 의해 브라운 운동의 첫 번째 통과 시점으로 독립적으로 사용되었다.재생 모델 분야에서 그것은 1940년에 그것을 설명한 Hugo Hadwiger의 뒤를 이어 Hadwiger 기능으로 알려져 있다.^[11]아브라함 월드는 이 분포를 순차 확률비 시험에서 표본의 제한적 형태로 1944년에^[12] 다시 도출했다.역가우스라는 이름은 1945년 모리스 트위디에 의해 제안되었다.^[13]트위디는 1956년과^[14] 1957년에^[15][16] 이 분포를 조사하여 통계적 특성 일부를 확립하였다.1978년 Peoples와 Chhikara가 배포를 광범위하게 검토했다.^[4]null

숫자 계산 및 소프트웨어

확률밀도함수에 대한 단순한 공식에도 불구하고, 역가우스 분포에 대한 수치확률 계산은 그럼에도 불구하고 모든 매개변수 값에 대한 부동소수점 산술에서 완전한 기계 정확도를 달성하기 위해 특별한 주의를 요한다.^[17]역 가우스 분포의 함수는 rmutil,^[18][19] SuppDists,^[20] STAR,^[21] invGauss,^[22] LaplacesDemon, ^[23]statmod를 포함한 여러 패키지에 의해 R 프로그래밍 언어에 제공된다.^[24]null

참고 항목

• 일반화된 가우스 역 분포
• 트위디 분포 -역 가우스 분포는 트위디 지수 분포 모델 계열의 구성원이다.
• 정지시간

참조

추가 읽기

• Høyland, Arnljot; Rausand, Marvin (1994). System Reliability Theory. New York: Wiley. ISBN 978-0-471-59397-3.
• Seshadri, V. (1993). The Inverse Gaussian Distribution. Oxford University Press. ISBN 978-0-19-852243-0.

외부 링크

• Wolfram 웹사이트의 Inverse Gaussian Distribution.