통계에서 가설 검증은 꼭 F-distribution 가장은 통계의 자연 일반화 샘플 통계의 세트의 분포는 발생하는으로 유명하다 연관되어 있다., Hotelling의T-squared 분포(T2), 해럴드 Hotelling,[1]이 제안한는 다변수의 확률 분포.운트 학생의 t-분배 를 방해하는 것.
Hoteling의 t-제곱 통계량 (t 2 다변량 가설 검정 에서 사용되는 학생의 t-통계학 을 일반화한 것이다.[2]
동기 분포는 (다변량) 모집단의 (다변량) 평균 간의 차이를 검정할 때 다변량 통계량 에서 발생하며, 여기서 일변량 문제에 대한 검정에서는 t-검정 을 사용할 수 있다. 이 분포는 학생 t 분포의 일반화로 개발한 Harold Hoteling 의 이름을 따서 명명되었다.[1]
정의 If the vector d {\displaystyle d} Gaussian multivariate-distributed with zero mean and unit covariance matrix N ( 0 p , I p , p ) {\displaystyle N(\mathbf {0} _{p},\mathbf {I} _{p,p})} M {\displaystyle M} p × p {\displaystyle p\times p} scale matrix and m degrees of freed 옴 (Wishart 분포 p m {\displaystyle W(\mathbf {I} _{p,p}m 2차 형식 displaystyle X} 파라미터 {\ displaystytyle p } 및 }) [3]
X = m d T M − 1 d ∼ T 2 ( p , m ) . [\displaystyle X=md^{ T}M^{-1}d\sim T^{2}(p,m) } 또한 임의 변수 X 에 Hoteling의 T-제곱 분포 X T 2 {\ displaystyle \sim T_{p,m}^{2}}, [1]
m − p + 1 p m X ∼ F p , m − p + 1 {\displaystyle {\frac {m-p+1}{pm}X\sim F_{p,m-p+1}:{p}} 여기서 F p m p {\ displaystyle F_{p,m-p+1} 매개변수 p와 m-p+1 이 있는 F-분포 다.
핫텔링 t-제곱 통계량 ^ ^ {\ displaystyle {\hat {\mathbf {\Sigma }}} 샘플 공분산 이 되도록
Σ ^ = 1 n − 1 ∑ i = 1 n ( x i − x ¯ ) ( x i − x ¯ ) ′ {\displaystyle {\hat {\mathbf {\Sigma } }}={\frac {1}{n-1}}\sum _{i=1}^{n}(\mathbf {x} _{i}-{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})'} 아포스트로피 에 의해 전치 된다는 뜻이지 ^ ^ displaystyle hat mathbf {\Sigma }}}}} [4] 양의 (세미) 한정 행렬이며 n 1 ^ displaystyle (n-1){\hatthebf Sigma }}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Wishart wishart wishart wishart wishart의 평균 ^ x x / displaystyle {\hatsbf {\\sigma }}}}{\mathbf {x}}}}}}}={\hat {\mathbf {\Sigma}}}}을(으 .
Hoteling의 t-제곱 통계량 은 다음과 같이 정의된다.[5]
t 2 = ( x ¯ − μ ) ′ Σ ^ x ¯ − 1 ( x ¯ − μ ) , {\displaystyle t^{2}=({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'{\hat {\mathbf {\Sigma } }}_{\overline {\mathbf {x} }}^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }}),} 표본 평균과 μ 거리 에 비례하는 값인 {\ displaystyle {\boldsymbol {\mu xμs {\ displaystyle {\\\mathbf {x}}}}\ \cH00\boldsymbol{\mu
분포 로 봤을 때.
t 2 ∼ T p , n − 1 2 = p ( n − 1 ) n − p F p , n − p , {\displaystyle t^{2}\심 T_{p,n-1}^{2}={\frac {p(n-1)}{n-p}F_{p,n-p}}} 여기서 F p n p {\ displaystyle F_{p,n-p} 매개변수 p 와 n - p 를 갖는 F-분포 다.
p-값 (여기서 p 변수와 무관함)을 계산하려면 t 2 {\ displaystyle t^{
n − p p ( n − 1 ) t 2 ∼ F p , n − p . {\displaystyle {\frac {n-p}{p(n-1)}}t^{2}\sim F_{p,n-p}} 그런 다음 왼쪽의 수량을 사용하여 F-분포에서 나오는 표본에 해당하는 p-값을 평가한다. 신뢰 영역 도 유사한 논리를 사용하여 결정할 수 있다.
동기 Let N p ( μ , Σ ) {\displaystyle {\mathcal {N}}_{p}({\boldsymbol {\mu }},{\mathbf {\Sigma } })} p -variate normal distributionlocation μ {\displaystyle {\boldsymbol {\mu }}} covariance Σ {\displaystyle {\mathbf {\Sigma } }}
x 1 , … , x n ∼ N p ( μ , Σ ) {\displaystyle {\mathbf {x}_{1},\dots, {\mathbf {x}}}\심 {\mathbal{N}_{p}({\boldsymbol {\mu},{\mathbf {\Sigma}}}}}}}}}}}}}} n개 의 독립적으로 분포된 (iid) 랜덤 변수 가 있으며, 이는 실제 숫자 1 {\displaystyle p\ properties 1} 정의
x ¯ = x 1 + ⋯ + x n n {\displaystyle {\mathbf {x}}}}}={\frac {\mathbf {x} _{1}+\cdots +\mathbf {x} _{n}}}}}} 공분산 x x σ {\displaystyle {\mathbf {\\sigma }}_{\cline mathbf {x}}}={\mathbf {\sigma }}}}}} 표본 평균임 을 나타낼 수 있다.
( x ¯ − μ ) ′ Σ x ¯ − 1 ( x ¯ − μ ) ∼ χ p 2 , {\displaystyle ({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'{\mathbf {\Sigma } }_{\overline {\mathbf {x} }}^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})\sim \chi _{p}^{2},} 여기서 χ p 2 {\ displaystyle \chi _{p}^{2}} p 인 카이 제곱 분포 다[6]
증명
증명 To show this use the fact that x ¯ ∼ N p ( μ , Σ / n ) {\displaystyle {\overline {\mathbf {x} }}\sim {\mathcal {N}}_{p}({\boldsymbol {\mu }},{\mathbf {\Sigma } }/n)} characteristic function of the random variable y = ( x ¯ − μ ) ′ Σ x ¯ − 1 ( x ¯ − μ ) = ( x ¯ − μ ) ′ ( Σ / n ) − 1 ( x ¯ − μ ) {\displaystyle \mathbf {y} =({\bar {\mathbf {x} }}-{\boldsymbol {\mu }})'{\mathbf {\Sigma } }_{\bar {\mathbf {x} }}^{-1}({\bar {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})=({\bar {\mathbf {x} }}-{\boldsymbol {\mu }})'({\mathbf {\Sigma } }/n)^{-1}({\bar {\mathbf {x} }}-{\bol dsymbol {\mathbf {\mu displaystyle \cdot } argument {\ displaystyle {\boldsymbol {\\Sigma }}}} 결정자 를 나타내도록.
특성 함수의 정의에 따라 다음이 있다.[7]
φ y ( θ ) = E e i θ y , = E e i θ ( x ¯ − μ ) ′ ( Σ / n ) − 1 ( x ¯ − μ ) = ∫ e i θ ( x ¯ − μ ) ′ n Σ − 1 ( x ¯ − μ ) ( 2 π ) − p / 2 Σ / n − 1 / 2 e − ( 1 / 2 ) ( x ¯ − μ ) ′ n Σ − 1 ( x ¯ − μ ) d x 1 ⋯ d x p {\displaystyle {\begin{aigned}\varphi _{\mathbf {y}}(\theta )&=\operatorname {E} e^{i\ta \mathbf {y}}}},\[5pt]&> =\operatorname {E} e^{i\theta ({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'({\mathbf {\Sigma } }/n)^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})}\\[5pt]& =\int e^{i\theta ({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'n{\mathbf {\Sigma } }^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})}(2\pi )^{-p/2} {\boldsymbol {\Sigma }}/n ^{-1/2}\,e^{-(1/2)({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'n{\boldsymbol {\Sigma }}^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})}\,dx_{1} \cdots dx_{p}\end{aigned}}} 적분 안에는 두 개의 지수(expective)가 있으므로 지수(expector)를 곱하여 다음과 같은 것을 얻는다.
= ∫ ( 2 π ) − p / 2 Σ / n − 1 / 2 e − ( 1 / 2 ) ( x ¯ − μ ) ′ n ( Σ − 1 − 2 i θ Σ − 1 ) ( x ¯ − μ ) d x 1 ⋯ d x p {\displaystyle {\begin{aligned}&=\int (2\pi )^{-p/2} {\boldsymbol {\Sigma }}/n ^{-1/2}\,e^{-(1/2)({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'n({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})}\,dx_{1}\cdots dx_{p}\end{aligned}}} Now take the term Σ / n − 1 / 2 {\displaystyle {\boldsymbol {\Sigma }}/n ^{-1/2}} I = ( Σ − 1 − 2 i θ Σ − 1 ) − 1 / n 1 / 2 ⋅ ( Σ − 1 − 2 i θ Σ − 1 ) − 1 / n − 1 / 2 {\displaystyle I= ({\boldsym bol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}/n ^{1/2}\;\cdot \; ({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}/n ^{-1/2}}
= ( Σ − 1 − 2 i θ Σ − 1 ) − 1 / n 1 / 2 Σ / n − 1 / 2 ∫ ( 2 π ) − p / 2 ( Σ − 1 − 2 i θ Σ − 1 ) − 1 / n − 1 / 2 e − ( 1 / 2 ) n ( x ¯ − μ ) ′ ( Σ − 1 − 2 i θ Σ − 1 ) ( x ¯ − μ ) d x 1 ⋯ d x p {\displaystyle{\begin{정렬}&^({\boldsymbol{\Sigma}}^{-1}-2i\theta{\boldsymbol{\Sigma}}^{-1})^{)}/n ^{1/2}{\boldsymbol{\Sigma}}/n ^{-1/2}\int(2\pi)^{-p/2}({\boldsymbol{\Sigma}}^{-1}-2i\theta{\boldsymbol{\Sigma}}^{-1})^{)}/n ^{-1/2}\,e^{-(1/2)n({\overline{\mathbf{x}}}-{\boldsymbol{\mu}})'({\boldsymbol{\Sigma}}^{)}-2.i\th eta {\boldsymbol {\Sigma }^{-1})({\overline {\mathbf {x}}-{\boldsymbol{\mu }}}\,dx_{1}\cdots dx_{p}\ended}}}}}}}}}} But the term inside the integral is precisely the probability density function of a multivariate normal distribution with covariance matrix ( Σ − 1 − 2 i θ Σ − 1 ) − 1 / n = [ n ( Σ − 1 − 2 i θ Σ − 1 ) ] − 1 {\displaystyle ({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}/n=\left[n ({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})\right]^{-1}} μ {\displaystyle \mu } x 1 , … , x p {\displaystyle x_{1},\dots ,x_{p}} 1 {\displaystyle 1} probability axioms .[clarification needed 따라서 다음과 같은 결과를 얻는다.
= ( Σ − 1 − 2 i θ Σ − 1 ) − 1 ⋅ 1 n 1 / 2 Σ / n − 1 / 2 = ( Σ − 1 − 2 i θ Σ − 1 ) − 1 ⋅ 1 n ⋅ n ⋅ Σ − 1 1 / 2 = [ ( Σ − 1 − 2 i θ Σ − 1 ) Σ ] − 1 1 / 2 = I p − 2 i θ I p − 1 / 2 {\displaystyle{\begin{정렬}&,=\left({\boldsymbol{\Sigma}}^{-1}-2i\theta{\boldsymbol{\Sigma}}^{-1})^{)}\cdot{\frac{1}{n}}\right ^{1/2}{\boldsymbol{\Sigma}}/n ^{-1/2}\\&,=\left({\boldsymbol{\Sigma}}^{-1}-2i\theta{\boldsymbol{\Sigma}}^{-1})^{)}\cdot{\frac{1}{\cancel{n}}}\cdot{\cancel{n}}\cdot{\boldsymbol{\Sigma}}^{.-1}\righ t ^{1/2}\\&=\left \left[({\cancel {{\boldsymbol {\Sigma }}^{-1}}}-2i\theta {\cancel {{\boldsymbol {\Sigma }}^{-1}}}){\cancel {\boldsymbol {\Sigma }}}\right]^{-1}\right ^{1/2}\\&= \mathbf {I} _{p}-2i\theta \mathbf {I} _{p} ^{-1/2}\end{aligned}}} 여기서 I p {\ displaystyle I_{p} 차원 {\displaystyle p} .
= ( 1 − 2 i θ ) − p / 2 {\displaystyle {\regated}&=(1-2i\theta )^{-p/2}\end{regated}}} 자유도 displaystyle 카이-제곱 분포 의 특성 함수. ◼ {\displaystyle \;\;\blacksquare }
2-표본 통계량 If x 1 , … , x n x ∼ N p ( μ , Σ ) {\displaystyle {\mathbf {x} }_{1},\dots ,{\mathbf {x} }_{n_{x}}\sim N_{p}({\boldsymbol {\mu }},{\mathbf {\Sigma } })} y 1 , … , y n y ∼ N p ( μ , Σ ) {\displaystyle {\mathbf {y} }_{1},\dots ,{\mathbf {y} }_{n_{y}}\sim N_{p}({\boldsymbol 표본이 같은 평균과 공분산을 가진 두 개의 독립적 인 다변량 정규 분포 로부터 독립적 으로 추출된 표본으로, {\mathbf {\Sigma }}} (
x ¯ = 1 n x ∑ i = 1 n x x i y ¯ = 1 n y ∑ i = 1 n y y i {\displaystyle {\overline {\mathbf {x} }}={\frac {1}{n_{x}}}\sum _{i=1}^{n_{x}}\mathbf {x} _{i}\qquad {\overline {\mathbf {y} }}={\frac {1}{n_{y}}}\sum _{i=1}^{n_{y}}\mathbf {y} _{i}} 표본의 평균으로,
Σ ^ x = 1 n x − 1 ∑ i = 1 n x ( x i − x ¯ ) ( x i − x ¯ ) ′ {\displaystyle {\hat {\mathbf {\Sigma } }}_{\mathbf {x} }={\frac {1}{n_{x}-1}}\sum _{i=1}^{n_{x}}(\mathbf {x} _{i}-{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})'} Σ ^ y = 1 n y − 1 ∑ i = 1 n y ( y i − y ¯ ) ( y i − y ¯ ) ′ {\displaystyle {\hat {\mathbf {\Sigma } }}_{\mathbf {y} }={\frac {1}{n_{y}-1}}\sum _{i=1}^{n_{y}}(\mathbf {y} _{i}-{\overline {\mathbf {y} }})(\mathbf {y} _{i}-{\overline {\mathbf {y} }})'} 각 표본 공분산 행렬로서. 그러면
Σ ^ = ( n x − 1 ) Σ ^ x + ( n y − 1 ) Σ ^ y n x + n y − 2 {\displaystyle {\hat {\mathbf {\Sigma } }}={\frac {(n_{x}-1){\hat {\mathbf {\Sigma } }}_{\mathbf {x} }+(n_{y}-1){\hat {\mathbf {\Sigma } }}_{\mathbf {y} }}{n_{x}+n_{y}-2}}} 편향되지 않은 합동 공분산 행렬 추정치(풀링된 분산 확장).
마지막으로 Hoteling의 2-표본 t-제곱 통계량은
t 2 = n x n y n x + n y ( x ¯ − y ¯ ) ′ Σ ^ − 1 ( x ¯ − y ¯ ) ∼ T 2 ( p , n x + n y − 2 ) {\displaystyle t^{2}={\frac {n_{x}n_{y}}{n_{x}+n_{y}}}({\overline {\mathbf {x} }}-{\overline {\mathbf {y} }})'{\hat {\mathbf {\Sigma } }}^{-1}({\overline {\mathbf {x} }}-{\overline {\mathbf {y} }})\sim T^{2}(p,n_{x}+n_{y}-2)} 관련개념 에[4]
n x + n y − p − 1 ( n x + n y − 2 ) p t 2 ∼ F ( p , n x + n y − 1 − p ) . {\displaystyle {\frac {n_{x}+n_{y}-p-1}{{y}-1}{(n_{x}+n_{y}-2}}:t^{2}\심 F(p,n_{x}+n_{y}-1-p) } 이 통계량의 Null이 아닌 분포는 중심 F-분포 (비중심 카이-제곱 랜덤 변수와 독립적인 중심 카이-제곱 랜덤 변수의 비율)이다.
n x + n y − p − 1 ( n x + n y − 2 ) p t 2 ∼ F ( p , n x + n y − 1 − p ; δ ) , {\displaystyle {\frac {n_{x}+n_{y}-p-1}{{y}-1}{(n_{x}+{y}-2}}:t^{2}\sim F(p,n_{x}+{y}+1-p;\delta }),} 와 함께
δ = n x n y n x + n y d ′ Σ − 1 d , {\displaystyle \cHB ={\frac {n_{x}n_{y}}}{n_{x}+n_{y}}}{n_{y}}}}}} }}}{\boldsymbol{d}'\mathbf {\Sigma }^{-1}{\boldsymbol {d},} 여기서 d y" {\ displaystyle {\d}=\mathbf {{\overline{x}-{\overline{y}}}}} (
2변수의 경우, 공식은 변수들 사이의 상관관계인 {\displaystyle \rho } ( 2 {\ displaystyle t^{2}} .
d 1 = x ¯ 1 − y ¯ 1 , d 2 = x ¯ 2 − y ¯ 2 {\displaystyle d_{1}={\overline {x}_{1}-{\overline {y}_{1},\qquad d_{2}={\overline {x}-{y}}}}}}} 그리고
s 1 = Σ 11 s 2 = Σ 22 ρ = Σ 12 / ( s 1 s 2 ) = Σ 21 / ( s 1 s 2 ) {\displaystyle s_{1}={\sqrt {\Sigma _{11}}}\qquad s_{2}={\sqrt {\Sigma _{22}}}\qquad \rho =\Sigma _{12}/(s_{1}s_{2})=\Sigma _{21}/(s_{1}s_{2})} 그때
t 2 = n x n y ( n x + n y ) ( 1 − r 2 ) [ ( d 1 s 1 ) 2 + ( d 2 s 2 ) 2 − 2 ρ ( d 1 s 1 ) ( d 2 s 2 ) ] {\displaystyle t^{2}={\frac {n_{x}n_{y}}{(n_{x}+n_{y})(1-r^{2})}}\left[\left({\frac {d_{1}}{s_{1}}}\right)^{2}+\left({\frac {d_{2}}{s_{2}}}\right)^{2}-2\rho \left({\frac {d_{1}}{s_{1}}}\right)\left({\frac {d_{2}}{s_{2}}}\right)\right]} Thus, if the differences in the two rows of the vector d = x ¯ − y ¯ {\displaystyle \mathbf {d} ={\overline {\mathbf {x} }}-{\overline {\mathbf {y} }}} t 2 {\displaystyle t^{2}} ρ {\displaystyle \rho } 반대 기호 t 2 {\ displaystyle ^{2}} ρ {\displaystyle \rho }
일변량 특례 는 웰치의 t-테스트에서 찾을 수 있다.
Hoteling의 2-표본 테스트보다 강력하고 강력한 테스트가 문헌에서 제안되었다. 예를 들어, 변수의 수가 피험자의 수와 비슷하거나 심지어 더 큰 경우에도 적용할 수 있는 중간 거리 기반 테스트를 참조하라.[8] [9]
참고 항목 참조 ^ a b c Hotelling, H. (1931). "The generalization of Student's ratio" . Annals of Mathematical Statistics 2 (3): 360–378. doi :10.1214/aoms/1177732979 ^ Johnson, R.A.; Wichern, D.W. (2002). Applied multivariate statistical analysis . 5 . Prentice hall. ^ 에릭 W. 와이스슈타인, 수학월드 ^ a b Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate Analysis . Academic Press. ISBN 978-0-12-471250-8 ^ "6.5.4.3. Hotelling's T squared" .^ 존슨, R.A. & Wichern, D.W. (2002 ) 제4.2장 끝^ Billingsley, P. (1995). "26. Characteristic Functions". Probability and measure (3rd ed.). Wiley. ISBN 978-0-471-00710-4 ^ Marozzi, M. (2016). "Multivariate tests based on interpoint distances with application to magnetic resonance imaging". Statistical Methods in Medical Research . 25 (6): 2593–2610. doi :10.1177/0962280214529104 . PMID 24740998 . ^ Marozzi, M. (2015). "Multivariate multidistance tests for high-dimensional low sample size case-control studies". Statistics in Medicine . 34 (9): 1511–1526. doi :10.1002/sim.6418 . PMID 25630579 .
외부 링크
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들

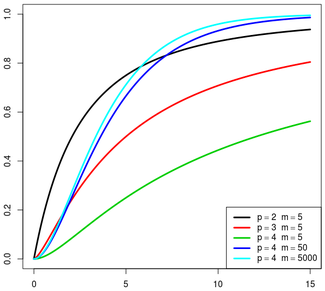







 Hoteling 분포(
Hoteling 분포(




 매개변수 p와 m-p+1이 있는
매개변수 p와 m-p+1이 있는 







 매개변수 p와 n - p를 갖는
매개변수 p와 n - p를 갖는 








 .
.



![{\displaystyle {\begin{aligned}\varphi _{\mathbf {y} }(\theta )&=\operatorname {E} e^{i\theta \mathbf {y} },\\[5pt]&=\operatorname {E} e^{i\theta ({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'({\mathbf {\Sigma } }/n)^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})}\\[5pt]&=\int e^{i\theta ({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'n{\mathbf {\Sigma } }^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mathbf {\mu } }})}(2\pi )^{-p/2}|{\boldsymbol {\Sigma }}/n|^{-1/2}\,e^{-(1/2)({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})'n{\boldsymbol {\Sigma }}^{-1}({\overline {\mathbf {x} }}-{\boldsymbol {\mu }})}\,dx_{1}\cdots dx_{p}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4f7443b5a91e8899f181974528a7d34bf9e047a)




![{\displaystyle ({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}/n=\left[n({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2e30acda26292ba3fcf5d6d302141d34fcebce5)



![{\displaystyle {\begin{aligned}&=\left|({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}\cdot {\frac {1}{n}}\right|^{1/2}|{\boldsymbol {\Sigma }}/n|^{-1/2}\\&=\left|({\boldsymbol {\Sigma }}^{-1}-2i\theta {\boldsymbol {\Sigma }}^{-1})^{-1}\cdot {\frac {1}{\cancel {n}}}\cdot {\cancel {n}}\cdot {\boldsymbol {\Sigma }}^{-1}\right|^{1/2}\\&=\left|\left[({\cancel {{\boldsymbol {\Sigma }}^{-1}}}-2i\theta {\cancel {{\boldsymbol {\Sigma }}^{-1}}}){\cancel {\boldsymbol {\Sigma }}}\right]^{-1}\right|^{1/2}\\&=|\mathbf {I} _{p}-2i\theta \mathbf {I} _{p}|^{-1/2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7b99da9756cc4c6b0312d41367697e0aa53eaca)
















![{\displaystyle t^{2}={\frac {n_{x}n_{y}}{(n_{x}+n_{y})(1-r^{2})}}\left[\left({\frac {d_{1}}{s_{1}}}\right)^{2}+\left({\frac {d_{2}}{s_{2}}}\right)^{2}-2\rho \left({\frac {d_{1}}{s_{1}}}\right)\left({\frac {d_{2}}{s_{2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdef78058fb5071adade5aaa4362df16e1b3747b)