다변량 정규 분포

다변량 정규 분포

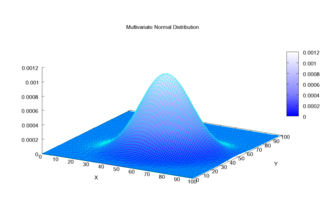
확률밀도함수 μ와 다변량 정규 분포에서 많은 샘플 포인트)[00]}=\left[{\begin{}smallmatrix 0\\0\end{smallmatrix}}\right]}과Σ)[13/53/52]}{\displaystyle{\boldsymbol{\Sigma}=\left는 경우에는{\begin{smallmatrix}1&, 3/5\\3/5&, 2\end{ 작은{\displaystyle{\boldsymbol{\mu}.매트릭스}}$\right$ 3각 타원, 2개의 한계 분포 및 2개의 1-d 히스토그램과 함께 표시됩니다.
표기법	$({displaystyle {n}}({\boldsymbol {mu}},{\boldsymbol {Sigma}})})$
파라미터	μ µk R :장소 δk × k δ R - 공분산(양반정의 행렬)
지지하다	x μ + span(δ) rk R
PDF	${\displaystyle \det(2\pi {Sigma }}^{-{\frac {1}{2}},\exp(-\frac {1}{2}) -{\boldsymbol {mu}}^{\!{\mathsf {T}}{\boldsymbol {Sigma}}^{-1}(\mathbf {x} - {\boldsymbol {mu }}),}}$ δ가 정의 정의일 때만 존재합니다.
의미하다	μ
모드	μ
분산	Σ
엔트로피	${\displaystyle {frac {1}{2}}\ln \det \left(2\pi \mathrm {e} {boldsymbol {Sigma }}\right}$
MGF	$\displaystyle \exp \!{\Big ( ) { \ bold symbol \ mu } ^{ !{\mathsf {T}}\mathbf {t} +{\tfrac {1}{2}}\mathbf {t}^{\!{\mathsf {T}}{\boldsymbol {Sigma}}\mathbf {t}{Big}}}$
CF	$\displaystyle \exp \!{\big ( ) i { \ bold symbol \ mu } ^{ } 。{\mathsf {T}}\mathbf {t}-{\tfrac {1}{2}}\mathbf {t}^{\!{\mathsf {T}}{\boldsymbol {Sigma}}\mathbf {t}{Big}}}$
쿨백-라이블러 발산	이하를 참조해 주세요

확률론과 통계학에서 다변량 정규분포, 다변량 가우스 분포 또는 합동 정규분포는 1차원 정규분포를 더 높은 차원으로 일반화한 것이다.한 가지 정의는 k 성분의 모든 선형 조합이 일변량 정규 분포를 갖는 경우 랜덤 벡터가 k-변수 정규 분포라고 하는 것입니다.그 중요성은 주로 다변량 중심 한계 정리에서 비롯된다.다변량 정규 분포는 각각이 평균 값 주위에 군집화되어 있는 (가능성이 있는) 상관된 실제 값 랜덤 변수 집합을 설명하는 데 자주 사용됩니다.

정의들

표기법 및 파라미터화

k차원 랜덤 $벡터{\displaystyle \mathbf{}}$ X $=$ ( ${\displaystyle {}_{}{}_{}}$1,${\displaystyle }$… , X${\displaystyle {}_{}{}^{}{k}_{}}$ )$$ {\$displaystyle \mathbf {X}$ =($X_{1},\ldots,X_{k})^{\mathrm {T}}}$의 다변량 정규 분포는 다음과 같은 표기법으로 쓸 수 있다.

${\displaystyle \mathbf {X} \sim \{mathcal {N}}({\boldsymbol {mu}},{\boldsymbol {Sigma}}}),}$

또는 X가 k차원임을 명확히 알리기 위해

${\displaystyle \mathbf {X} \sim \{mathcal {N}}_{k}({\boldsymbol {mu}},{\boldsymbol {Sigma }}),}$

k차원 평균 벡터를 사용하여

${\displaystyle {\boldsymbol {mu}}=[\mathbf {X}]=(\operatorname {E}[X_{1}),\ldots,\operatorname {E}[X_{k})^{\textbf {T}},}$

$및{\displaystyle }$k ×$$ {$displaystyle$ k$\times$ k$}$ 공분산 행렬

$\displaystyle \Sigma _{i,j}=\operatorname {E}[(X_{i}-\mu _{i})(X_{j}-\mu _{j})]=\operatorname {Cov}[X_{i,X_{j}}}}$

1${\displaystyle i}$ i${\displaystyle ,}$ ${\displaystyle j}$ ${\displaystyle \le }$ $.$ {{$displaystyle 1\leq$ i$,j\leq$k.} 공분산$$ 행렬의 역행렬을 ${\displaystyle {\mathrm{정밀도}}^{}}$ 행렬이라고 하며, $Q{\displaystyle \mathit{}}$ ${\displaystyle {}^{}}$ {\displaystyle ${$Q} = boldsymbol ${$Q} ${{-1$로 나타낸다.

표준 정규 랜덤 벡터

실제 랜덤 $벡터{\displaystyle \mathbf{}}$ X $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle ...}$, ${\displaystyle X_{}{}^{}}$k ) ${\displaystyle {T\mathrm{}}^{}}$ ${\$ =($X_{1},\ldots,X_{k})^{\mathrm {T}$}}}는 성분 ${\displaystyle X_{}}$k {\$displaystyle X_{$k$$}}가 모두 독립적이고 각 단위가 0일 때 표준 정규 랜덤 벡터라고 불린다.${\displaystyle {}_{}}$$~$${\displaystyle }$$N{\displaystyle }$ ( $0$${\displaystyle }$,${\displaystyle 1}$) \ $style$ X _ { $k$$$} \$sim$\ \ $mathcal${ $N$} （$0$ , $1$$$$）$^{[1]: p. 454} 。

중심 정규 랜덤 벡터

실제 랜덤 $벡터{\displaystyle \mathbf{}}$ X $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle ...}$ , ${\displaystyle {}_{}{}^{}{k}_{}}$ ) ${\displaystyle {T\mathrm{}}^{}}$ ${\$$displaystyle$ $\mathbf {X}$ =($X_{1},X_{k})^{\mathrm {T}}}$는 $결정론적{\displaystyle }$k ×$$\$display$ k\times$$\$ell}$ $행렬$이 존재하는 경우 중심 정규 랜덤 벡터라고 합니다$.$$dsymbol {A}}\mathbf {Z}$은 X$$$${\$displaystyle \mathbf {X}}$ 와$$ $같은{\displaystyle \mathbf{}}$ 분포를 가집니다.$여기$서 Z${\displaystyle$ \$mathbf {$Z$} }$ 는 {\^{[1]: p. 454} $${\$displaystyle \ell }$ 성분의$$ 표준 정규 랜덤 벡터입니다.

정규 랜덤 벡터

실수 랜덤 $벡터{\displaystyle \mathbf{}}$ X $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle ...}$ , ${\displaystyle {}_{}{}^{}{k}_{}}$ ) ${\displaystyle {T\mathrm{}}^{}}$ ${\$ =($X_{1},\ldots,X_{k})^{\mathrm {$$T$$}$$$}}}는 랜덤$\ell {\displaystyle }$ {\$displaystyle$\ell$\}$ - Z$$ $displaystyle$ {$mathbf}$} } a there a \ \ \ \ \ \ \ \mathbf} } a} a} a} a \ a}}}}} \ \} \mathbf {{{{{{{{{$또는{\displaystyle }$${\displaystyle \mu \mathit{}}$(\$displaystyle \mathbf {A$$})$ 및 $k{\displaystyle }$×$$${\displaystyle \ell }$(\$displaystyle$ k$\times\$$ell$$)$ $행렬$ A$displaystyle \mathbf {X} = boldsymbol {A}) 행렬$ A$(\$ {A})

형식:

여기서 공분산 행렬은 ${\displaystyle \delta \mathit{}}$ $=$ $T${\$displaystyle$ {\$boldsymbol {Sigma$}}= $boldsymbol {A}$ {\$boldsymbol {A}}$ {\$mathrm {T$ 입니다.

공분산 행렬이 특이할 경우 해당 분포에는 밀도가 없습니다. 자세한 내용은 아래 절을 참조하십시오.이 경우는 통계량, 예를 들어 정규 최소 제곱법에서 잔차 벡터의 분포에서 자주 발생합니다.$(\$})는 일반적으로 독립적이지 않습니다$.$ 독립$$가우스 $변수$ Z(\displaystyle $\mathbf {Z$ 컬렉션에 $행렬{\displaystyle \mathit{}}$ A(\displaystyle$\boldsymbol {A})$를 적용한 결과라고 볼 수 있습니다.

동등한 정의

다음 정의는 위에 제시된 정의와 동일합니다.랜덤 $벡터{\displaystyle \mathbf{}}$ X $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle ...}$ , ${\displaystyle X_{}{}^{}}$k )$$ {\$displaystyle \mathbf {X}$ =($X_{1},\ldots,X_{k}^{$$T}}:$ 다음$$ 동등한 조건 중 하나를 만족하는 다변량 정규 분포를 가집니다.

• 각 성분들의 $선형{\displaystyle }$ 조합 ${\displaystyle {}_{}}$ $=$ ${\displaystyle {}_{}{}_{}}$ X 1 +${\displaystyle {\theta }_{}}$ + k ${\displaystyle {}_{}{}_{}}$ {\$displaystyle$ Y$=a_{1$}X_${1}+\cdots +a_${k}X_${k}}$는 정규 분포를 따릅니다.즉, 임의의 상수 $벡터{\displaystyle \mathbf{}}$ a${\displaystyle {}^{}}$ R $k$\$displaystyle$ \$mathbf {a}$ \$in \mathbb {R$$}$$$^{\$mathbf {a}$= ${\displaystyle T^{}\mathbf{}}$ X$^{\displaystyle$ Y=\$mathbf$ {$T}}$} \$mathbf {X}$ }에$$ 대해 랜덤 $변수{\displaystyle }$ Y ${\displaystyle =}$는 정규 분포를 가진다.
• $(\$$\mathbf\$$mu })$와 대칭 $$의${\displaystyle }$k ×$$(\$displaystyle$k\$times$k$)$ 행렬$$$\delta {\displaystyle \mathbf{}}$(\$displaystyle\boldsymbol\Sigma$ $})$가 있으며$,$ $X$의 $특징{\displaystyle \mathbf{}}$ 함수는 $다음$과 같다.
  $$\displaystyle \varphi _{\mathbf {X}(\mathbf {u})=\exp {Big(}i\mathbf {u})^{T}{\tfrac {1}{2}}\mathbf {u}{\mathbf} }}$$

  

구면 정규 분포는 성분이 직교 ^[3][4]좌표계에서 독립적인 고유한 분포로 특징지을 수 있습니다.

밀도 함수

비퇴행성 케이스

다변량 정규 분포는 대칭 공분산 행렬 $(\$style$\display\boldsymbol\Sigma })$가 양수이면 "비퇴화"라고 한다.이 경우 분포는 밀도가^[5] 있습니다.

$여기$서 x$(\$는 실제 k차원 열 벡터이고 $($는 det$(\$의 결정 변수입니다.위의 방정식은$\delta {\displaystyle \mathbf{}}$(\$displaystyle\boldsymbol\Sigma})$가 1${\displaystyle }$×$$(\$displaystyle$ 1$\times$1) $행렬$(즉, 단일 실수)인 경우 일변량 정규 분포로 감소합니다.

복잡한 정규 분포의 원형 대칭 버전은 약간 다른 형태를 가집니다.

각 Iso-density 궤적(각각 밀도의 특정 값을 제공하는 k차원 공간 내 점의 궤적)은 타원 또는 그 고차원 일반화이다. 따라서 다변량 정규 분포는 타원 분포의 특수한 경우이다.

$양$(${\displaystyle \sqrt{x\mathit{}}}$ -${\displaystyle \sqrt{{}^{\mu \mathrm{}}}}$ ) ${\displaystyle \sqrt{{T\Omega }^{}{\mathbf{}}^{}}}$-${\displaystyle \sqrt{{}^{}{1}^{}}}$ (${\displaystyle \sqrt{}}$x -${\displaystyle \sqrt{\mu \mathit{}}}$ $){$ $displaystyle${ $sqrt${ ( \ $mathbf { x$} } - { \ $boldsymbol${$$t$$} }{ \ $mathrm${ $T$} } { \ $boldsymbol$} }${$ - $1$} { \ $symboldsymbol }$$$ $k$ ${\displaystyle =<img\; alt="\{\backslash boldsymbol\backslash mu\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/a1aee7d7b4a36d96dfb35bfee9c7751bba1fdfbe"\; style="vertical-align:\; -0.671ex;\; width:1.646ex;\; height:2.009ex;">}$ ${\displaystyle 1}${\$displaystyle$$k$$=1$일 때 분포는 일변량 정규 분포로 감소하고 마할라노비스 거리는 표준 점수의 절대값으로 감소합니다.아래의 간격도 참조하십시오.

이변량 케이스

2차원 비싱글 케이스(${\displaystyle }$ ${\displaystyle =}$ ${\displaystyle \mathrm{랭크}}$ ${\displaystyle (}$ (${\displaystyle \mathrm{\sigma }}$ ) ${\displaystyle =}$ \ $display$ k = \$operatorname {rank$} \$left$ ( \$Sigma$ \ right ) $= 2$ $$)에서 벡터 [${\$ \ style \ text {$$}의 확률 밀도 함수$XY$ ]$$}} } } :

${\displaystyle f(x,y)=flac {1}{2\pi \pi _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}\exp \flac {2 (1-\rho ^{2}}}}}}}\left[\fleftwrac {\frac {\frac {{{{{{{{x}}}}}}}}}}}}}}}{\frac {2}}}}}}}}}}$

$여기$서 ${\$ { $displaystyle$$\rho$}는$$$X$와 의$상관관계$이며$,$ X> 0 \ $displaystyle$ \$sigma$_ { $X$} > 0 및 Y$>$ \ $displaystyle$ \$sigma$_ { $Y$}>$0$ 입니다.이 경우,

$(\displaystyle {\boldsymbol {mu }=pmatrix}\mu _{X}\mu _{Y}\end{pmatrix}},\quad {\boldsymbol {Sigma}}=pmatrix _{2}\rambol _{X}\r}\r},\rho \rho \mboldsigmboldsy_{{{{{\},\mbr},\mbr},\mbr},\mbr},\}$

이변량의 경우, [$]$의 벡터가 $정상$이라고 결론짓기 위해 X$(\$$displaystyle$ X$)$와 Y(\$displaystyle$ Y$)$의 여러 개별 선형 조합이 정상임을 확인하기에 충분하기 때문에 다변량 정규성 재구성을 위한 첫 번째 등가 조건을 덜 제한적으로 만들 수 있다.$텍스트$$XY]}}}}$은(는) ^[6]이변량 정규입니다.

x${\displaystyle }$,$$ , y , \ $displaystyle x$, y - 평면에$$ 표시된 이변량 iso-density loci는 타원형이며, 주축은 공분산 행렬$\delta {\displaystyle \mathbf{}}$ \ $display$\ $style$ \$symbol$ \ Sigma $}$ $$(타원의 주 및 부 반변량 반변수들은 순서 고유값의 제곱근과 동일)의 고유 벡터에 의해 정의된다.

상관 파라미터$$δ(\$displaystyle\rho)$의 절대값이 증가함에 따라 이들 로키는 다음 행으로 압축됩니다.

${\displaystyle y(x)=\operatorname {sgn}(\rho){\frac _{Y}}{\sigma _{X}}(x-\mu _{X})+\mu _{Y}}.}$

${\displaystyle 이}$는 ${\displaystyle \mathrm{sgn}}$ ${\displaystyle (}$ ( ${\displaystyle )}$ $){$ $displaystyle \operatorname {sgn}(여기서$sgn은 부호함수)이 $"{$$displaystyle$ $\rho$로 대체된 이 표현식이 X$\displaystyle$ X$"$^[7]의 $값$이 주어진 Y$\display$ Y의 $최적$의 선형 불편 예측이기 때문입니다.

퇴화 케이스

공분산 행렬$\delta {\displaystyle \mathbf{}}$(\$displaystyle\boldsymbol\Sigma}})$가 풀 랭크가 아닌 경우 다변량 정규 분포는 퇴화되어 밀도가 없습니다.더 정확히는 k차원 르베게 측정(미적분 수준 확률 코스에서 가정하는 일반적인 측정)에 대한 밀도가 없습니다.측정치와 관련하여 분포가 절대적으로 연속적인 랜덤 벡터만 밀도가 있다고 한다.밀도에 대해 설명하되 측정이론적인 복잡성을 다루지 않으려면$$x $좌표$의 부분 집합 ${\displaystyle (}$ ($$$style$ ) \$displaystyle \operatorname$ {rank } ( \ $boldsymbol$\$$$Sigma$$}$ )로 주의를 제한하여 이 부분 집합의 공분산 행렬이 양의 행렬이 되도록 하는 것이 더 간단할 수 있다.다른 좌표는 선택된 좌표의 ^[8]아핀 함수로 간주할 수 있다.

단일한 경우에 밀도에 대해 의미 있게 이야기하려면 다른 기본 척도를 선택해야 합니다.분해정리를 사용하여 가우스 분포가 지원되는 $k$의 ({displaystyle \$mathbb$ {R$}$$^{$k$$$})$ -차원$$ 아핀 부분 공간 $(({$displaystyle$\mathbb {R$} ^{k})$${${\displaystyle e\mathit{}}$ +${\displaystyle {\mu \mathbf{}}^{}\})}$까지 르베그 측정의 제한을 정의할 수 있다$.{\displaystyle }$$R$ k $}$ { $displaystyle$ \ { \ $bold symbol$\ { \ $sigma$^ { $1$/ $2$} } $}$ \ $mathbf { v$} : \$mathbb$ { $R$}$$$^$ { k } \ } 。이 측정에 대한 분포의 밀도는 다음과 같습니다.

${\displaystyle f(\mathbf {x})=bladfrac {e^{-{\frac {1}{2}}(\mathbf {x}-{\boldsymbol {mu}}})^{\!{\mathsf {T}}{\boldsymbol {Sigma }^{+}(\boldsymbol {x} - {\boldsymbol {mu}}}}}{\sqrt {(2\pi}^{k}\det \nolimitsymboldsymbol {}}}}}}}}}}}}}}}}}}}}{{{{{{{{\}}}}}}}}}}}}}}}}}}}}}}}}$

$여기$서${\displaystyle {}^{}}$δ$$+({$displaystyle${{$Sigma }}^{+})$는 일반화 역,$$k({$displaystyle$$$k$})$는$\delta {\displaystyle \mathbf{}}$({$displaystyle$ {$Sigma}})$의 $순위{\displaystyle }$, ${\displaystyle {}^{}}$t$({$ det$^{*}}}})$는 의사 결정자입니다.^[9]

누적분포함수

차원 1의 누적분포함수(cdf)의 개념은 직사각형 및 타원형 영역에 기초한 다차원 사례로 두 가지 방법으로 확장될 수 있다.

첫 번째 방법은 랜덤 $벡터{\displaystyle \mathbf{}}$X(\displaystyle $\mathbf {X}$$$^[10]$}$의 $cdf{\displaystyle }$ F$)$ {$displaystyle$ F$(\mathbf {x})$를 X$(\$의 모든 성분이 벡터$$x(\$displaystyle$ {$x})$의 대응하는 값 이하일 확률로 정의하는 것입니다.

${\displaystyle F(\mathbf {x})=\mathbb {P}(\mathbbf {X}),\mathbf {X}\sim {mathcal {N}}({\boldsymbol {mu}},{\boldsymbol {Sigma}}})입니다.}$

F${\displaystyle }$( ${\displaystyle x\mathbf{}}$) \ $displaystyle$ F ( \ $mathbf { x }$ $)$에는 닫힌 형식이 없지만 수치로 ^[10][11]추정하는 알고리즘이 많이 있습니다.

또 다른 방법은 $cdf{\displaystyle }$ F$)$ {$displaystyle$ F$(r)}$를 표준편차의 ^[12]직접적인 일반화인 가우스로부터의 마할라노비스 $거리{\displaystyle }$r(\$displaystyle$r)에$$ 의해 결정된 타원체 내부에 샘플이 존재할 확률로 정의하는 것입니다.이 함수의 값을 계산하기 위해 다음과 같은 닫힌 해석식이 존재한다.^[12]

간격

다변량 정규 분포의 구간은 다음을 만족하는 벡터 x로 구성된 영역을 산출합니다.

${\displaystyle({\mathbf {x}}-{\boldsymbol {mu }})^{T}{\boldsymbol {Sigma}}^{-1}({\mathbf {x}-{\boldsymbol {mu}})\leq \chi _{k}^2}(p)}$

$여기$서 x$({$는 k$(\displaystyle$k) 차원 벡터, $\mu$(\displaystyle\boldsymbol\mu})는 $(\displaystyle$ k$)$ 차원$$ 평균 벡터,$$$displaystyle\syle$\sigmbol\sigmbol\$sigma$ $})$는 알려진 공분산 행렬입니다.{$k}^{2}(p)}$은 k${$^[13]$displaystyle$ k$}$를 갖는 카이스트 분포의 $확률{\displaystyle }$ p${displaystyle$ p$}$에 대한 분위수 함수입니다$.$$k{\displaystyle }$ ${\displaystyle =\mathrm{2일}}$ 때$({displaystyle$ k$=2,})$ 식은$$ 타원의 내부를 정의하고 카이스트 분포는 평균이 2인 지수 분포로 단순화됩니다(속도는 절반).

상보 누적 분포 함수(꼬리 분포)

상보적 누적분포함수(ccdf) $또는$ 꼬리분포는 $F{\displaystyle \stackrel{}{}}$ ${\displaystyle (}$ (${\displaystyle x\mathbf{}}$ )${\displaystyle =}$ ${\displaystyle 1\mathbf{}}$- ${\displaystyle P\mathbb{}}$ ( X${\displaystyle x\mathbf{}}$x$$) \ $style$( \ $mathbf${ $F$} )$=$ 1 - \ $mathbbb$ {$P }$( \ $mathbf {$ X${\displaystyle }$$}$ )로 ${\displaystyle 정의}$됩니다$.${\$boldsymbol {Sigma$ ccdf는 종속 가우스 변수의 ^[14]최대값 확률로 기술할 수 있습니다$.$

${\displaystyle {F}(\mathbf {x})=\mathbb {P}(\cup_{i}\geq x_{i}\})=\mathbb {P}(\max_{i})Y_{i}\geq 0),\quad {text{where}}\mathbf {Y}\sim {mathcal {N}}({\boldsymbol {mu}}}-\mathbf {x},{\boldsymbol {Sigma}})}$

ccdf 계산을 위한 간단한 닫힌 공식은 존재하지 않지만, 몬테 카를로 ^[14][15]방법을 통해 의존적인 가우스 변수의 최대값을 정확하게 추정할 수 있다.

특성.

다른 도메인에서의 확률

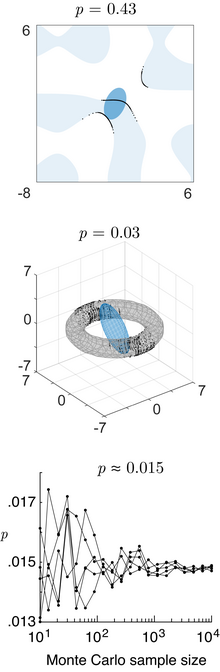
x+q0을은 다변량 정상의 이차 도메인의 확률 콘텐츠 q())에 의해 정의되))′Q2x+q1′;0{\displaystyle q({\boldsymbol{x}})={\boldsymbol{)}}'\mathbf{Q_{2}}{\boldsymbol{)}}+{\boldsymbol{q_{1}}}'{\boldsymbol{)}}+q_{0}>. 0}일 경우(어디 Q2{\displaystyle \mathbf{.Q_{2}}$$}은$$ ${\displaystyle {행렬\mathbf{}}_{}}$,$$q $1({displaystyle {q_{$1$$}})은 ${\displaystyle {벡터\mathrm{}}_{}}$,$$q 0({$displaystyle q_{$0$$})은 스칼라)는 가우스 판별분석을 이용한 베이지안 분류/결정 이론과 관련된 행렬이며 일반화 카이 제곱 ^[16]분포에 의해 주어진다$.$f( { $displaystyle$ f ( { \ $boldsymbol${ x } > $0$} ($여기$서${\displaystyle }$f (${\displaystyle x\mathit{}}$) { $style$ f ( { \ $boldsymbol {x}}$ ) > 0 )로 정의되어 있는 임의의 일반 도메인내의 확률 컨텐츠는, 레이 트레이스(Matlab 코드)의 수치 방법을 사용해 계산할 수 있습니다.

모멘트를 높이다

x의 k차 모멘트는 다음과 같습니다.

$\displaystyle \mu _{1,\ldots,N}(\mathbf {x})\stackrel {r_{1},\ldots,r_{N}(\mathbf {x})\stackrel {mathbrm {def}{=}\opername {E}\stackrf}_j}$

여기서₁ r + r₂ + + + r_N = k 입니다.

k차 중심 모멘트는 다음과 같습니다.

여기서 합계는 세트${\displaystyle }${${\displaystyle 1\mathrm{},\dots ,}$ ${\displaystyle 2}$ $}$의 모든 할당({$displaystyle \left\{1,\ldots,2\displayda \right\})$을 ((순서 없는) 쌍으로 가져옵니다.즉, k번째(= 2µ = 6) 중심 모멘트의 경우, δ = 3 공분산의 곱을 합한다. (기대값 μ는 근소한 값으로 0으로 간주됨):

${\displaystyle{\begin{정렬}&,\operatorname{E}[X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}]\\[8pt]={}&,\operatorname{E}[X_{1}X_{2}]\operatorname{E}[X_{3}X_{4}]\operatorname{E}[X_{5}X_{6}]+\operatorname{E}[X_{1}X_{2}]\operatorname{E}[X_{3}X_{5}]\operatorname{E}[X_{4}X_{6}]+\operatorname{E}[X_{1}X_{2}]\operatorname{E}[X_{3}X_{6}]\operat.orname{E}[X_{4}X_{5}]\\[4pt]&,{}+\operatorname{E}[X_{1}X_{3}]\operatorname{E}[X_{2}X_{4}]\operatorname{E}[X_{5}X_{6}]+\operatorname{E}[X_{1}X_{3}]\operatorname{E}[X_{2}X_{5}]\operatorname{E}[X_{4}X_{6}]+\operatorname{E}[X_{1}X_{3}]\operatorname{E}[X_{2}X_{6}]\operatorname{E}[X_{4}X_{5}]\\[4pt]&,{}+\operatorname{E}[X_{1}X_{4}]\op.eratorna나[X_{2}X_{3}]\operatorname{E}[X_{5}X_{6}]+\operatorname{E}[X_{1}X_{4}]\operatorname{E}[X_{2}X_{5}]\operatorname{E}[X_{3}X_{6}]+\operatorname{E}[X_{1}X_{4}]\operatorname{E}[X_{2}X_{6}]\operatorname{E}[X_{3}X_{5}]\\[4pt]&,{}+\operatorname{E}[X_{1}X_{5}]\operatorname{E}[X_{2}X_{3}]\operatorname{E}[X_{4}X_{6}]+\operatorname{E}.{E}[X_{1}X_{5}]\operatorname{E}[X_{2}X_{4}]\operatorname{E}[X_{3}X_{6}]+\operatorname{E}[X_{1}X_{5}]\operatorname{E}[X_{2}X_{6}]\operatorname{E}[X_{3}X_{4}]\\[4pt]&,{}+\operatorname{E}[X_{1}X_{6}]\operatorname{E}[X_{2}X_{3}]\operatorname{E}[X_{4}X_{5}]+\operatorname{E}[X_{1}X_{6}]\operatorname{E}[X_{2}X_{4}]\operatorname{E}는 경우에는 X_.{3}X_{5}+\operatorname {E} [X_{1}X_{6}\operatorname {E}[X_{2}X_{5}\operatorname {E}[X_{3}X_{4}].\end { aligned}}$

$({\displaystyle \frac{}{}}$ 2 ${\displaystyle \frac{2}{}}$-${\displaystyle \frac{1}{}}$ ${\displaystyle \frac{)!}{2^{}}}$ ${\displaystyle \frac{{-}^{}}{}}$- ${\displaystyle \frac{1}{}}$ (${\displaystyle \frac{-}{}}$- 1 $)!\$ $displaystyle${$tfrac${ ($2$ \ $lambda$ -$$1 )!$}{2^{\contda-1}(\contda-1)!$$}}}$개의$$ 합계항(위의 경우 15)으로 각각 v(이 경우 3)공분산의 곱이다.4차 모멘트(4개 변수)의 경우 세 개의 항이 있습니다.6차 모멘트의 경우 3 × 5 = 15 항이 있고, 8차 모멘트의 경우 3 × 5 × 7 = 105 항이 있다.

그런 다음 목록${\displaystyle }$[${\displaystyle 1,\dots ,}$ $]({displaystyle [$1,\$ldots,$2\$lambda])$의 용어를 r, r, r₂ 등으로 구성된₁ 목록의 해당 용어로 대체하여 공분산을 결정합니다.이것을 설명하기 위해서, 다음의 4차 중심 모멘트 케이스를 조사합니다.

${\displaystyle{\begin{정렬}\operatorname{E}\left[X_{나는}{4}^\right]&, =3\sigma _ᆱ^ᆲ\\[4pt]\operatorname{E}\left[X_{나는}^{3}X_{j}\right]&, =3\sigma _{ii}\sigma _ᆵ\\[4pt]\operatorname{E}\left[X_{나는}{2}X_{j}^{2}\right^]&, =\sigma _{ii}\sigma _{jj}+2\sigma _ᆹ^ᆺ\\[4pt]\operatorname{E}\left[X_{나는}{2}X_{j}X_{k}^\right]&, =\sigma._{ii}\sigma_{jk}+2\sigma _{ik}\[4pt]\operatorname {E}\left[X_{i}X_{j}X_{n}\right]&=\sigma _{ij}\sigma _{k}+\sigma _{k}_{k}\sigma_{k}_{j}_{n}_{n}_{k}_{n}_{n}_{n}_n}_n}_n}_n}_n}_n}_sigma}_n}\end { aligned}}$

여기서 ${\displaystyle i_{}}$ i$$ \$displaystyle \sigma$ _${ij}$는 X와_j X의_i 공분산입니다.위의 방법에서는 먼저 K개의 다른 X 변수${\displaystyle (}E{\displaystyle }$ [ ${\displaystyle X{}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle j_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle x_{}}$ x${\displaystyle {}_{}}$x n$$]\$displaystyle E\left$ [$X_{i]$X_${j}X_{k}X_{n}\$right$])$를 사용하여 k번째 모멘트의 일반적인 대소문자를 찾은 후 그에 따라 단순화합니다.예를 들어 ${\displaystyle {}_{}^{}}$ ${\displaystyle [}$ [ X ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle X_{}}$ ${\displaystyle {}_{}{}_{}}$ X $]{$ $displaystyle \operatorname { E$}[ $X$_ { $i } X _$ { $k$} $\}$의_j $경우{\displaystyle \mathrm{}}$ X = X ${\displaystyle {}_{}^{}}$_i ${\displaystyle i_{}}$ ${\displaystyle 2_{}^{}}$ { \$style$ \ { n }$$\$2222$222 2 $222 =$ 2 \$stylestylestyle2222222222222222222222$ 2 2222222 2 2 2 2222222 2 2 2 2 2 2 2 $222222222$

정규 벡터의 함수

정규 $벡터{\displaystyle \mathit{}}$x({style ${x$${\displaystyle }q{\displaystyle }$ (${\displaystyle x\mathit{}\})}$ $=$ ${\displaystyle {}^{}q{\mathbf{}}_{}}$ Q ${\displaystyle {2\mathbf{}}_{}{{\mathit{}}_{}}^{}}$ + ${\displaystyle {{q\mathbf{}}_{}}^{}}$ ${\displaystyle 1\mathit{}{{}_{}}^{}+}$ ${\displaystyle {}_{}}$ + ${\displaystyle {q\mathrm{}}_{}}$0 ({$displaystyle$q\\$boldsymbol$ {x}})="$x"\mathbf {Q_{2}}\boldsymbol {1}$의 2차 형식$매트릭스{\displaystyle {\mathit{}}_{}}$ ${\displaystyle {q\mathbf{}}_{}}$ 1$({$은 $벡터$이고 ${\displaystyle {q\mathrm{}}_{}}$ 0$({$ style $q_{0}$은 스칼라)은 일반화 카이 변수입니다.^[16]

f$)$ {$displaystyle$ f$({\boldsymbol {x}})}$가 정규 벡터의 일반적인 스칼라값 $함수$라면, 그 확률밀도함수, 누적분포함수 및 역 누적분포함수는 광선추적법(Matlab 코드)^[16]으로 계산할 수 있다.

우도 함수

평균 및 공분산 행렬이 알려진 경우 관측 $벡터{\displaystyle \mathit{}}$ x$(\$의 로그 우도는 확률 밀도 함수의 로그일 뿐이다.

$μ$$$,

z$\$가 복소수 벡터인 비중심복합 케이스의 원형 대칭 버전은 다음과 같습니다.

${\displaystyle \ln L({\boldsymbol {z})=-\ln({\boldsymbol {Sigma}}}{\boldsymbol {z}})^{\boldsymbol {z})^{-1}({\boldsymboldsymbol {z})$

즉, 켤레 전치(indicated$\displaystyle\$displaystyle$)$를 사용하여 일반 전치(indicated$\$를 바꿉니다.복잡한 정규 분포의 원형 대칭 버전은 정규화 상수에 대해 약간 다른 형태를 가지기 때문에 실제와 약간 다릅니다.

다중 선형 ^[17]회귀 분석에도 유사한 표기법이 사용됩니다.

정규 벡터의 로그 우도는 정규 벡터의 2차 형식이므로 일반화 카이 제곱 ^[16]변수로 분포됩니다.

미분 엔트로피

다변량 정규 분포의^[18] 미분 엔트로피는 다음과 같습니다.

${\displaystyle {displaystyle}h\left(f\right)&=-\int _{-\infty}^{\infty}^{\infty}^{\infty}{\infty}f(\mathbf {x})\lnf,^{k}\left {\boldsymbol {Sigma}}\right\frac {k}\ln \left(2\pi e\right)+{\frac {1}{2}\ln \left(\left {\boldsymbol {Sigma}}}}\right \frac {2}\fright}$

여기서 막대는 행렬 행렬 행렬식을 나타내고 k는 벡터 공간의 차원도를 나타냅니다.

쿨백-라이블러 발산

N1(μ 1,1Σ){\displaystyle{{N\mathcal}}_ᆭ({\boldsymbol{\mu}}_{1},{\boldsymbol{\Sigma}}_{1})}에서 N0으로 그 Kullback–Leibler 발산({\displaystyle{{N\mathcal}}_ᆯ({\boldsymbol{\mu}}_{0}일 경우,{\boldsymbol{\Sigma}}_{0})},non-singular 매트릭스의와 Σ0은Σ1.:[19]

${\displaystyle D_{\text{KL}({\mathcal {N}}_{0}\{})={1 \over2}\left\{\operatorname {tr} \leftsymbol {\sigma }}_{1} {\boldsygmbol {0} {\}} {\} {\} {\} {\} {\} {\} {\}} {\} {\light}ymbol {Sigma}}_{1}\over {bold symbol {Sigma}}_{0}\right\}$

$여기$서 k$\displaystyle$k는$$ 벡터 공간의 치수입니다.

로그 뒤에 오는 두 개의 항 자체가 밀도 함수의 요소이거나 자연적으로 발생하는 식의 기저 e 로그이기 때문에 로그는 반드시 기저 e를 사용해야 합니다.따라서 이 방정식은 nats 단위로 측정된 결과를 나타냅니다.위의 식 전체를 로그2로_e 나누면 비트 단위의 편차가 발생합니다.

${\displaystyle {\mathit{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{}}_{}}$0일 $({style$ {$boldsymbol {mu$}}_${$1} =$boldsymbol {mu$}}$_{0$

$\displaystyle D_{\text{KL}({\mathcal {N}}_{0}\{})={1\over2}\left\{\operatorname {tr}\boldsymbol {\Sigma }}_{1}{\boldsymbol {0}}{{{\}}}}{{{{\}}}}}}}}{오른쪽}}}}}}}}}}$

상호 정보

분포의 상호 정보는 쿨백-라이블러 발산(Kullback-Leibler divergence)의 특수한 경우이며$,$ $여기$서 P(\$displaystyle$ P$)$는 완전 다변량 $분포$이고$$Q(\$displaystyle$ Q$)$는 1차원 한계 분포의 산물이다.이 문서의 Kullback-Leibler 발산 섹션의 ${\displaystyle {}_{}}$에서 δ1(style$\$$_$${1})$은 대각선$$엔트리가$(\displaystyle\sigma$이고 ${\displaystyle {\mathit{}}_{}}$ $μ0$(\$display\sigmbold_mbol\$symbol\symbol\symb)인 대각선행렬입니다.$$상호 정보의 공식은 다음과 같습니다.

${\displaystyle I({\boldsymbol {X}})=-{1 \over 2)\ln {\boldsymbol {rho}}_{0},}$

여기서 ${\displaystyle {\mathrm{}}_{}}$0 \ $displaystyle$ { \ bold $symbol${ $rho } _$ {$$$0$ } the$$$$ 0 \ $displaystyle${ \ $sigma } _$_ { 0$$^{[citation needed]}} where construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct construct

이변량의 경우 상호정보에 대한 표현은 다음과 같다.

${\displaystyle I(x;y)=-{1 \over 2)\ln(1-\rho ^{2}).}$

관절 정규성

정규 분포 및 독립적

$X(\displaystyle$ X$)$와 Y$(\displaystyle$ Y$)$가 정규 분포로 독립되어 있는 $경우{\displaystyle }$ 이는 "공동 정규 분포"를 의미합니다. 즉, 쌍$, Y)$은 다변량 정규 분포를 가져야 합니다.단, 공동 정규 분포 변수 쌍은 독립적일 필요가 없습니다(관련되지 않은 경우에만 해당). $\theta {\displaystyle }$ ${\displaystyle =}$ $(\displaystyle \rho$=$0)$

정규 분포 랜덤 변수 두 개가 공동으로 이변량 정규 분포일 필요는 없습니다.

2개의 랜덤 $변수{\displaystyle }$X(\$style$ X$)$와 Y$(\displaystyle$ Y$)$가 모두 정규 분포를 갖는다고 해서 쌍$,$ $)$의 정규 분포를 갖는 것은 아닙니다.단순한 예로는 X가 기대치가 0이고 분산이 1인 정규 분포를 $가지며{\displaystyle }$ X> \ $displaystyle$X$$> $c$}이면 Y ${\displaystyle =}$$X$$$\ $displaystyle$ Y$=$ - $X$（ ） >$0 display$ $style$Y= - X $。$세 개 이상의 랜덤 변수에 대해 유사한 반례가 있습니다.일반적으로 이러한 합계는 혼합물 ^{[citation needed]}모형에 해당합니다.

상관관계와 독립성

일반적으로 랜덤 변수는 상관 관계가 없지만 통계적으로 종속될 수 있습니다.그러나 랜덤 벡터에 다변량 정규 분포가 있으면 상관 관계가 없는 두 개 이상의 성분이 독립적입니다.즉, 쌍으로 독립되어 있는 두 개 이상의 성분이 독립적이라는 것을 의미합니다.그러나 위에서 지적한 바와 같이 정규 분포와 상관 관계가 없는 두 개의 랜덤 변수가 독립적이라는 것은 사실이 아닙니다.

조건부 분포

N차원 x가 다음과 같이 분할된 경우

$\displaystyle \mathbf {x} = displaystyle {bmatrix} \ mathbf {x} _ {1} \ \ \ \ mathbf { x } { \ text { size } { \ times 1 \ \ \ （ N - q ） \ times 1 \ }$

따라서 μ와 δ는 다음과 같이 구분된다.

$(\displaystyle {\boldsymbol {mu } = bmatrix } {\boldsymbol {mu } _ {1} \ {\boldsymbol {mu } } {\end {bmatrix} } {\text {크기} q\times 1\times 1\\\\(N-q)\\\\end {matrix} } } } } } } } } }$

$(\displaystyle {\boldsymbol {Sigma}}={bmatrix}{\boldsymbol {Sigma}}_{11}&{\boldsymbol {Sigma}}}}_{12}\{\{\boldsigma }}}&{\boldsymbol {trix}{textsigmb}}{textsymb}{text}}{text}{trix}{text}{trix}}}$

그러면 x = a에₂ 대한 x 조건부₁ 분포는 다변량 정규 분포(x₁₂ x = a) ~ N(μ, δ)이다.

${\displaystyle {\bar {\boldsymbol {\mu} = {\boldsymbol {\sigma}}_{12} {\boldsymbol {\sigma}}} {{-1} \left(\mathbf {a} - {\boldsymbol {\mu}} {{{{{{{}}}}} {{{{{{{{{{{1}}}}}}}}}} {{{{{{{{{{{{{{{{{$

및 공분산 행렬

${\displaystyle {\boldsymbol {\Sigma}={11}-{\boldsymbol {\Sigma}}_{12}{{-1}{\boldsymbol {\Sigma}}_{21}.}$^[20]

${\displaystyle {\mathrm{\sigma }}_{}^{}}$ 22${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$（ $style ）$ { style }{ $22$$$} $_$$${ $22$$}$ ${\displaystyle {\mathrm{the<img\; alt="\backslash boldsymbol\backslash Sigma\_\{22\}^\{-1\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/5645b3cb0e657d54c5fda043cb0d614b4c740031"\; style="vertical-align:\; -1.005ex;\; width:4.264ex;\; height:3.343ex;">}}_{}}$ the the inverse of of of $of$ of （ \ style ）의 일반화 역수입니다.행렬 $\sigma {\displaystyle \stackrel{}{\mathbf{}}}$σ σ ${\displaystyle \stackrel{}{\{\backslash }}$ （ \ $sigma }$$$） $here$ here here here₂₂ here here here here here here here here here here here $here$ of of here here {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ {\ of {\ {\ {\ {\ {\ {\ {\ {\ {\ of of of of of of즉, 위의 방정식은 전체 공분산 행렬을 반전시키고, 조건화할 변수에 해당하는 행과 열을 삭제한 다음, 조건부 공분산 행렬을 얻기 위해 역반전하는 것과 같습니다.

그것이 미국)는 가변성을 바꾸는 것을 알면서도 새로운 분산은 의 특정 값에 의존하지 않는다 아마도 더욱 놀라운 것은, 평균Σ 12Σ 22− 1(한− μ 2){\displaystyle{\boldsymbol{\Sigma}}_{12}{\boldsymbol{\Sigma}}_{22}^{)}\left(\mathbf{를}-{\boldsymbol{\mu}}_{2}\rig 이동합니다.h$t$ ; 이 값을 a의 값을 모르는 상황과 비교합니다.이₁ 경우 x의 ${\displaystyle {분포}_{}}$는$($ ${\displaystyle {\mathbf{}}_{}}$,${\displaystyle {}_{}{\mathrm{\delta }}_{}}$ 11$$)(\$displaystyle${\$mathcal {N}}_{q}\$left$({\boldsymbol$ {$mu }}_{$1},{\$boldsymigma }}}$ {$11\$right$\}).$

이 결과를 증명하기 위해 도출된 흥미로운 사실은 랜덤 $벡터{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ 2$({$$}$ $_{2})$와 ${\displaystyle {\mathrm{}}_{}}$ 1 $=$ ${\displaystyle {}_{}{\mathrm{}}_{}}$ -$$ 12$$ 22${\displaystyle {}_{}^{}}$- ${\displaystyle {}_{}^{}{\mathbf{}}_{}}$ ({$displaystyle \mathbf {y} _{1}-{\boldsyolgmb}$ {$Sigma}$ {$12$})이다$.$움푹 패이다

행렬 δ는₁₂₂₂⁻¹ 회귀 계수의 행렬로 알려져 있습니다.

이변량 케이스

x가 $({$과 ${\displaystyle {X2\mathrm{}}_{}}$$({$$displaystyle X_{$$2$$\})$로 분할되어 있는 이변량의 ${\displaystyle {경우\mathrm{}}_{}}$ X2({$displaystyle X_{$1})의^[21] $조건부{\displaystyle {}_{}}$ 분포는 다음과 같습니다.

$({displaystyle X_{1}\mid X_{2}=a\sim \\mathcal {N}\left(\mu _{1}+{\frac {1}}){\rho(a-\mu _{2}), (1-\rho ^{2})\rho _{1}\rho{{2}\rh}\rh}\fright(오른쪽)}$

$여기$서 ${\({displaystyle \rho})$는 $({$과 $({$ $사이$의 상관계수입니다.

이변량 조건부 기대치

일반적인 경우

${\displaystyle {\begin{pmatrix}X_{1}\X_{2}\end{pmatrix}\sim {\begin{pmatrix}\left({\begin{pmatrix}\mu_{2}\end{pmatrix}\rigma}\rigma_1\s$

X가₂ 주어질 때 X의 조건부₁ 기대치는 다음과 같습니다.

${\displaystyle \operatorname {E}(X_{1}\mid X_{2}=x_{2})=\mu _{1}+\rho {\frac _{1}{\frac _{2}}(x_{2}-\mu _{2})$

증명: 위의 조건부 $분포{\displaystyle {}_{}}$ ${\displaystyle {X1\mathrm{}}_{}{}_{}}$ ${\displaystyle {X2\mathrm{}}_{}}$({$displaystyle X_{1}\mid$ X_${2})$의 예상을 취함으로써 결과를 얻을 수 있습니다.

단위 분산이 있는 중심화된 경우

${\displaystyle {\begin{pmatrix}X_{1}\X_{2}\end{pmatrix}\sim {\begin{pmatrix}0\end{pmatrix}}, {\begin{pmatrix}1&\rho\end{pmatrix}}오른쪽}}$

X가₂ 주어질 때 X의 조건부₁ 기대치는

$\displaystyle \operatorname {E}(X_{1}\mid X_{2}=x_{2})=\rho x_{2}}$

그리고 조건부 분산은

$\displaystyle \operatorname {var} (X_{1}\mid X_{2}=x_{2})=1-\rho ^{2};}$

따라서 조건부 분산은 x에 의존하지₂ 않습니다.

X가₂ z보다 작거나 클 때 X의 조건부₁ 기대치는 다음과 같습니다.^{[22]: 367}

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}<z)=-\rho {phi(z)\over \Phi(z)}$

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}>z)=\rho {phi(z)\over(1-\Phi(z)}}$

여기서 마지막 비율을 역밀스 비율이라고 합니다.

증명: ${\displaystyle {}_{}}$ 2개의 결과는 E ${\displaystyle (}$ ( X ${\displaystyle {}_{}{}_{}{2\mathrm{}}_{}}$ ${\displaystyle {X\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {x\mathrm{}}_{}}$ 2) ${\displaystyle =}$ ${\displaystyle {}_{}}$x ${\displaystyle {2\mathrm{}}_{}}$ ( \ $displaystyle$ \$operatorname${ $E$} ( X _ {$1}$ \ $mid X$ _ {2} = \$rho$x $_ {$2}$$=\$rho$ x _ {2}} )를 사용하여 얻을 수 있습니다.

( 1 X < ) $=$ ( 2 X <) \ $displaystyle \operatorname { E$}($X_{1}\mid$ X_${2$}<z)=\$rho$ E$(X_{2}\mid X_2}<z)$ 및 예측 속성을 사용합니다.

한계 분포

다변량 정규 랜덤 변수의 부분 집합에 대한 한계 분포를 얻으려면 평균 벡터와 공분산 행렬에서 관련 없는 변수(외부화하려는 변수)를 삭제하기만 하면 됩니다.이에 대한 증거는 다변량 정규 분포와 선형 ^[23]대수의 정의에서 나옵니다.

예

X = [X₁, X₂, X₃]를 평균 벡터 μ = [μ₁₂, μ₃, μ] 및 공분산 행렬 δ(다변량 정규 분포에 대한 표준 모수화)를 갖는 다변량 정규 랜덤 변수라고 가정합니다.′ Σ 그리고 X′)[X1, X3]다변수의 비열한 벡터로 보통이다 μ′의 결합 분포)[μ1, μ3]과 공분산 행열)[Σ 11Σ 13Σ 31Σ 33]{\displaystyle{\boldsymbol{\Sigma}}'={\begin{bmatrix}{\boldsymbol{\Sigma}}_{11}&,{\boldsymbol{\Sigma}}_{13}\\{\boldsymbol{\Sigma}}_{31일}.&{\bold$기호 {Sigma}}_{33)\end{bmatrix$

아핀 변환

Y = c + BX가 X${\displaystyle }$~ ${\displaystyle N(\mu \mathit{}}$ ${\displaystyle ,\delta \mathbf{}}$)의 아핀 변환$(\displaystyle \mathbf {X}$ \$sim {\boldsymbol {N}},${\$boldsymbol${\$sigma$}}), 여기서 c는${\displaystyle }M{\displaystyle }$ × $(\style)$의 벡터 $상수입니다$$.$기대 가치와 Rmal 유통 댁+Bμ과 차이 BΣBT 즉, Y번 국도 N(댁+Bμ, BΣ BT){\displaystyle \mathbf{Y}\sim{{N\mathcal}}\left(\mathbf{c}+\mathbf{B}{\boldsymbol{\mu}},\mathbf{B}{\boldsymbol{\Sigma}}\mathbf{B}^{\rm{T}}\right)}. 특히 자이의 어떤 부분 집합은 미약한 페닜다는다변량 정규 분포이기도 합니다.이것을 확인하려면 , 다음의 예를 검토해 주세요.서브셋(X₁, X₂, X₄)^T을 추출하려면 , 다음과 같이 합니다.

${\displaystyle \mathbf {B} = beginb { bmatrix }1&0&0&\ldots & 0\\0&1&0&\ldots & 0\end {bmatrix}$

원하는 요소를 직접 추출합니다.

또 다른 결론은 Z = b · X의 분포입니다.여기서 b는 X와 같은 수의 원소를 가진 상수 벡터이고 점은${\displaystyle Z}$~ N(${\displaystyle {\mathrm{}}^{}{\mathbf{}}^{},}$ ${\displaystyle T^{}\mathbf{}}$ ${\displaystyle \delta \mathbf{}}$ b$)\displaystyle Z\sim$ {$N}\left(\mathbfcdot)$입니다.$\boldsymbol {Sigma }}\mathbf {b}\right$이 결과는 다음과 같습니다.

$\displaystyle \mathbf {B} = scap{bmatrix}b_{1}&b_{2}&\ldots & b_{n}\end{bmatrix}=\mathbf {b}^{\rm {T}}}.}$

δ의 양의 정의성이 도트 곱의 분산이 양의 값이어야 한다는 것을 암시하는 것을 관찰합니다.

2X와 같은 X의 아핀 변환은 X의 두 독립 실현의 합과 같지 않다.

기하학적 해석

비단일 다변량 정규 분포의 등밀도 등고선은 ^[24]평균에 중심을 둔 타원체(즉, 초구체의 선형 변환)이다.따라서 다변량 정규 분포는 타원 분포 클래스의 한 예입니다.타원체의 주축 방향은 공분산 행렬$\delta {\displaystyle \mathbf{}}$(\$displaystyle\boldsymbol\Sigma$ $\})$의 고유 벡터에 의해 주어진다.주축의 상대 길이 제곱은 해당 고유값에 의해 제공됩니다.

δ = U^T = U δ^1/2(U^1/2)^T가 단위 고유 벡터이고 δ가 고유 값의 대각 행렬인 경우, 다음과 같이 됩니다.

${\displaystyle \mathbf {X} \sim {mathcal {N} \sim {\boldsymbol {\sigma}} \iff \mathbf {X} \sim \boldsymbol {U} + mathbda } {Cal } {1}}$

또, 축을 반전해도 N(0, δ)에는 영향이 없기 때문에 U를 회전행렬로 선택할 수 있지만, 열을 반전해도 U의 행렬식 부호가 변화한다.분포 N(μ, δ)은 실질적으로 N(0, I)으로 δ 스케일링되고^1/2 U로 회전하며 μ로 환산된다.

반대로 μ, 풀랭크 매트릭스 U 및 양의 대각선 엔트리 δ_i 중 하나를 선택하면 비단수 다변량 정규 분포를 얻을 수 있습니다.δ가_i 0이고 U가 제곱인 경우 결과 공분산^T 행렬 U δU는 특이합니다.기하학적으로 이것은 모든 등고선 타원체가 무한히 얇고 n차원 공간에서는 부피가 0임을 의미합니다. 이는 적어도 하나의 주축의 길이가 0이기 때문입니다. 이것이 퇴화 사례입니다.

극좌표(반경 및 각도)로 다시 작성된 이변량 정규 랜덤 변수에서 참 평균 주위의 반지름은 호이트 ^[25]분포를 따릅니다.

1차원에서는${\displaystyle }$μ ±$$(\$displaystyle\mu\$pm$\sigma})$ $구간$에서 정규 분포의 샘플을 찾을 확률은 약 68.27%이지만, 고차원에서는 표준 편차 타원 영역에서 샘플을 찾을 확률은 낮다.^[26]

치수	확률
1	0.6827
2	0.3935
3	0.1987
4	0.0902
5	0.0374
6	0.0144
7	0.0052
8	0.0018
9	0.0006
10	0.0002

통계적 추론

모수 추정

다변량 정규 분포의 공분산 행렬에 대한 최대우도 추정기의 도출은 간단합니다.

즉, 다변량 정규 분포의 확률 밀도 함수(pdf)는 다음과 같습니다.

${\displaystyle f(\mathbf {x})=bandfrac {1}{(2\pi)^{k}{\boldsymbol {Sigma}}}}\exp \leftsymbol {1 \over2}(\mathbf {x})^{\rm {T}}{1-sigmboldsigm } } } } } } } }$

n개의 관측치 표본에서 공분산 행렬의 ML 추정치는 다음과 같습니다.

${\displaystyle {\mathbf {x} {\mathbf {x} } = {1 \overn} \sum _{i=1}^{n} ({\mathbf {x} } } } {\overline {\mathbf {x} } } } {\mathbf {x} } } } } } ^{{{{\line } } } } } } } } } } } } } ^{\lineT}}$

이것은 단순히 표본 공분산 행렬입니다.이것은 기대치가 다음과 같은 편향된 추정치입니다.

$(\displaystyle E[{\widehat {\symbol {Sigma }}}=bladfrac {n-1}{n}}{\boldsymbol {Sigma}}}}).}$

치우치지 않은 표본 공분산은 다음과 같습니다.

$X ]{ display$$ac {1}{n-1}\left[X'\left(I-{\frac {1}{n}\cdot$ J$\right)X\right]($행렬 형식$,$ $I{\displaystyle }$ {\$displaystyle$ I$}$는${\displaystyle }K{\displaystyle }$ ×$K$$\$$times$ K$\$times K\$times$ 매트릭스), J는${\displaystyle }$K ×$K$ × $KTimes 매트릭스$입니다.

다변량 정규 분포의 모수를 추정하기 위한 Fisher 정보 행렬에는 닫힌 형식 식이 있습니다.예를 들어 이 설정을 사용하여 파라미터 추정을 위한 Cramér-Rao 경계를 계산할 수 있습니다.상세한 것에 대하여는, Fisher 의 정보를 참조해 주세요.

베이지안 추론

베이지안 통계에서 평균 벡터 앞의 켤레는 또 다른 다변량 정규 분포이고, 공분산 행렬 앞의 켤레는 역위샤트 $분포{\displaystyle {\mathcal{}}^{}}$W -$$({$displaystyle {W}}^-1})$이다. n개의 관측치가 이루어졌다고 가정하자.

${\displaystyle \mathbf {X} =\{\mathbf {x} _{1},\display,\mathbf {x} _{n}\sim {n}}({\boldsymbol {mu}},{\boldsigmbol {Sigma}}}})$

그리고 우선 활용사가 배정되었다면

$({displaystyle p}, {\boldsymbol {Sigma}}=p4\boldsymbol {{Sigma}}}\mid {\boldsymbol {Sigma}}})\p4\boldsymbol {Sigma}}},$

어디에

$\displaystyle p({\boldsymbol\mu}}\mid\mathcal {N}({\boldsymbol\mu}}_{0},m^{-1}{\boldsymbol\sigma}})$

그리고.

${\displaystyle p({\boldsymbol {Sigma })\sim {\mathcal {W}}^{-1}({\boldsymbol {Psi }}}, n_{0}).}$

그러면...^{[citation needed]}

${\displaystyle{\begin{배열}({\boldsymbol{\mu}}\mid{\boldsymbol{\Sigma}},\mathbf{X})&, \sim&{{N\mathcal}}\left({\frac{n{\bar{\mathbf{x}}}+m{\boldsymbol{\mu}}_{0}}{n+m}},{\frac{1}{n+m}}{\boldsymbol{\Sigma}}\right),\\p({\boldsymbol{\Sigma}}\mid \mathbf{X})&, \sim&{{W\mathcal}}^{)}\left({\boldsymbol{\Psi}}.+n\mathbf{S}+{\frac {nm}{n+m}({\bar {mathbf {x}}})-{\boldsymbol {mu}}_{0})({\bar {\boldsymbol {mu}}}_{0}), n+n_{0}\right,\end{array}}})$

어디에

${\displaystyle {\mathbf {x} {\mathbf {x} {\mathbf {S} &=mathbf {x} _{i},\mathbf {S} &=mathbf {1} {n} \sum _i=1} {{n}(\mathbf {x} {x} _sum frac {n}\end { aligned}}$

다변량 정규성 검정

다변량 정규성 검정은 주어진 데이터 집합에서 다변량 정규 분포와 유사성을 검사합니다.귀무 가설은 데이터 집합이 정규 분포와 비슷하므로 p-값이 충분히 작으면 비정규 데이터를 나타냅니다.다변량 정규성 검정에는 Larry Rafsky와 Jerome ^[29]Friedman이 만든 Cox-Small^[27] 검정과 Smith와 Jain의 Friedman-Rafsky 검정이 포함됩니다^[28].

Mardia의 검정은^[30] 왜도 및 첨도 측도의 다변량 확장을 기반으로 합니다.k차원 벡터의 샘플 {x₁, ..., x}에_n 대해 계산한다.

$(\displaystyle {displaystyle {boldsymbol {Sigma } = {1 \over n} \sum _{j=1}^{n} \ left ( \ mathbf {x} - { \ bar \ mathbf { x} } ) \ left ( \ mathbf { x} )T}\\&A={1 \over 6n}\sum _{i=1}^{n}\sum _{j=1}^{n}\left[(\mathbf {x}_{i}-{\bar {mathbf {x}}}})^{T}\;{\widehat {\boldsymbol {Sigma }^{-1}({j}-{\bar {\mathbf {x}})\right] {{3}\&B=sqrt {8k(k+2}}}}\\\\{1\oversum}_bfright = nsum{T}\;{\widehat {\boldsymbol {Sigma }}^{-1}(\mathbf {x}_{i}-{\bar {x}})\right]^2}-k(k+2)\right\}\end{aligned}}}}$

다변량 정규성의 공 가설에 따라 통계적인 것은 A.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-outp로 대략은 카이 제곱 분포를 가질 것이다.다고.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output 자유의 .sr-onlyᆮ1(k+1)(k+2)도, B가 대략 표준 정상 N(0,1).

마르디아의 첨도 통계량은 치우쳐져 있으며 제한된 정규 분포로 매우 느리게 수렴됩니다.중간 크기 표본< $)$ {$displaystyle (50\leq$n < $400$의 경우 첨도 통계량의 점근 분포 모수가 수정되고^[31] 소규모 표본 검사(< \$displaystyle$n <$50$) 경험적 임계값이 사용됩니다.렌처는^[32] k = 2, 3, 4에 대해 두 통계량에 대한 임계값 표를 제공한다.

마르디아의 테스트는 아핀 불변성이지만 일관성은 없다.예를 들어, 다변량 왜도 검정이 대칭 비정규 ^[33]검정과 일치하지 않습니다.

BHEP 테스트는^[34] 정규 분포의 경험적 특성 함수와 이론적 특성 함수 사이의 차이에 대한 규범을 계산합니다.노름의 계산은 가우스 가중 $함수{\displaystyle {}_{}}$ ${\displaystyle {\mu }_{}}$β ( ${\displaystyle t\mathbf{}}$)${\displaystyle {}^{}=}$ ( ${\displaystyle 2}$ ${\displaystyle {}^{}{}^{}{\beta \mathrm{}}^{}}$ 2 )${\displaystyle {}^{}}$- k /${\displaystyle {2\mathbf{}}^{}}$ e -${\displaystyle {{}^{\mathrm{}}2}^{}}$ / ( ${\displaystyle {{}^{}}^{}}$ ${\displaystyle {{\beta \mathrm{}}^{}}^{}}$ $){$ $display \ mu _$ { \ t } ( \ $mathbf${ t } ) $=$( 2 \$pi$ \ ^ { ^ 2 ) / $k$/ { 2 ^ 2$^2$ $}$에 대하여 제곱적분함수의 L ($μ$) 공간에서² 행해진다.테스트 통계는

$디스플레이 스타일T_{\beta}&,=\int _{\mathbb{R}^{k}}\left{n1\over}\sum _{j=1}^{n}e^{i\mathbf{t}^{T}{\widehat{\boldsymbol{\Sigma}}}^ᆳ(\mathbf{x}_{j}-{\bar{\mathbf{x})}}}-e^{-\mathbf{t}^{2}/2}\right ^{2}\,{\boldsymbol{\mu}}{t}\\& _ᆸ(\mathbf{t})\,d\mathbf, ={1\over n^{2}}\sum _{i,j=1}^{n}e^{-{\beta ^{2}\over 2}(\mathbf{)}_{.나는}-\mathbf {x} _{j})^{T}{\widehat {\boldsymbol {\Sigma }^{-1}(\mathbf {x} _{i}-\mathbf {x} _{j})-{\frac {2}{k/2}\sum _{i=1}^{n}e^{{{j}}}{frac 2}}{{{frac}}}}{{frc}}}}}{{n}}}}{frc}{n}}}}}{n}}{n}{n}}}}}}{T}{\widehat {\boldsymbol {Sigma }}^{-1}({i}-{\bar {mathbf {x}})+{\frac {1}{(1+2\beta ^{2}}}^{k/2}}\end{aligned}}}}}$

이 검정 통계량의 한계 분포는 카이 제곱 랜덤 ^[34]변수의 가중치 합이지만, 실제로는 몬테카를로 ^{[citation needed]}시뮬레이션을 사용하여 표본 분위수를 계산하는 것이 더 편리합니다.

이러한 테스트 절차 및 기타 테스트 절차에 대한 자세한 조사를 ^[35]이용할 수 있습니다.

다변량 정규 등급으로 분류

가우스 판별 분석

관측치(벡터)가 알려진 평균과 공분산을 가진 여러 다변량 정규 분포 중 하나에서 나온다고 가정합니다.그런 다음 주어진 관측치를 발생 확률이 가장 높은 분포에 할당할 수 있습니다.이 분류 절차를 가우스 판별 분석이라고 합니다.분류 성능, 즉 다른 분류 결과의 확률과 전체적인 분류 오류는 수치적 광선 추적 방법(Matlab 코드)으로 계산할 수 있다.

계산 방법

분포에서 값 그리기

N차원 다변량 정규분포에서 평균 벡터 μ 및 공분산 행렬 δ를 사용하여 랜덤 벡터 x를 추출(샘플링)하는 데 널리 사용되는 방법은 ^[36]다음과 같이 작동합니다.

1. A^T = Ω인 실행렬 A를 구한다.δ가 양의 확정일 경우, 일반적으로 콜레스키 분해가 사용되며, 이 분해의 확장된 형태는 항상 사용할 수 있다(공분산 행렬이 양의 반정의 것일 수 있으므로). 두 경우 모두 적절한 행렬 A를 얻을 수 있다.대안으로 δ의 스펙트럼 분해 δ = U⁻¹ δU에서 얻은 매트릭스 A = U^½ δ를 사용한다.전자의 접근방식은 계산적으로 더 간단하지만 행렬 A는 랜덤 벡터 요소의 다른 순서에 따라 변경되며, 후자의 접근방식은 단순한 재순서로 관련된 행렬을 제공한다.이론적으로 두 접근법 모두 적절한 행렬 A를 결정하는 데 동일한 좋은 방법을 제공하지만, 계산 시간에는 차이가 있다.
2. z = (z₁, …, z_N)^T 성분이 N개의 독립적인 표준 정규 변수인 벡터라고 가정합니다(예를 들어, 박스-뮬러 변환을 사용하여 생성할 수 있습니다).
3. x를 μ + Az로 합니다.이것은 아핀 변환 속성으로 인해 원하는 분포를 가집니다.

「 」를 참조해 주세요.

• 카이 분포, 다변량 정규 분포 벡터(비상관 및 제로 중심)의 2-노름(유클리드 노름 또는 벡터 길이)의 pdf입니다.
  • Rayleigh 분포, 이변량 정규 분포 벡터(비상관 및 제로 중심)의 벡터 길이 pdf
  • 쌀 분포, 이변량 정규 분포 벡터(비상관 및 비중심)의 벡터 길이 pdf
  • 호이트 분포, 이변량 정규 분포 벡터(상관 및 중심)의 벡터 길이 pdf
• 이변량 정규 분포의 적용인 복소 정규 분포
• 코풀라, 가우스 또는 일반 코풀라 모델의 정의를 위한 것입니다.
• 다변량 t-분포, 이것은 또 다른 널리 사용되는 구형 대칭 다변량 분포입니다.
• 지수(특성 함수에서 지수)가 0과 2 사이인 경우 다변량 정규 분포의 다변량 안정 분포 확장입니다.
• 마할라노비스 거리
• 위샤트 배포
• 행렬 정규 분포

레퍼런스

문학.