확률 분포

통계에 관한 시리즈의 일부
확률론
확률 악리 결정론 시스템. 부정론 랜덤성
확률 공간 샘플 공간 이벤트 종합적인 이벤트 초급 이벤트 상호 배타성 결과 싱글턴 실험. 베르누이 재판 확률 분포 베르누이 분포 이항 분포 정규 분포 확률 측도 랜덤 변수 베르누이 과정 연속 또는 이산 기대치 마르코프 연쇄 관측치 랜덤 워크 확률 과정
보충 이벤트 결합 확률 한계 확률 조건부 확률
인디펜던스 조건부 독립성 확률의 법칙 대수의 법칙 베이즈 정리 불의 부등식
벤도 트리 다이어그램
v t

확률 이론과 통계학에서 확률 분포는 실험에 ^[1][2]대해 다른 가능한 결과의 발생 확률을 주는 수학 함수이다.표본 공간과 사건의 확률(표본 ^[3]공간의 부분 집합) 측면에서 무작위 현상에 대한 수학적인 설명입니다.

예를 들어 동전 던지기("실험")의 결과를 나타내기 위해 X를 사용하는 경우 X의 확률 분포는 X = 앞면의 경우 0.5(2 또는 1/2의 1), X = 뒷면의 경우 0.5(동전이 공정하다는 의미)를 취합니다.무작위 현상의 예로는 미래의 날씨 조건, 무작위로 선택된 사람의 키, 학교의 남학생 비율, 실시해야 할 조사 결과 ^[4]등이 있다.

서론

확률 분포는 표본 공간의 부분 집합인 사건의 확률에 대한 수학적인 설명입니다.표본 공간은 종종 $denoted{\displaystyle \mathrm{}}$\$displaystyle \Omega$로$$표시되며, 관찰되는 랜덤 현상의 가능한 모든 결과의 집합입니다.실수 집합, 벡터 집합, 임의의 비숫자 값 집합 등 모든 집합일 수 있습니다.예를 들어, 동전 던지기 샘플 공간은 δ = {앞면, 뒷면}입니다.

특정 랜덤 변수의 경우(표본 공간을 숫자 집합으로 볼 수 있도록)에 대한 확률 분포를 정의하려면 이산형 랜덤 변수와 절대 연속형 랜덤 변수를 구분하는 것이 일반적입니다.이산적인 경우에는 각각의 가능한 결과에 확률을 할당하는 확률 질량 $함수{\displaystyle }$ p$\displaystyle$p를$$ 지정하면 된다.예를 들어 공평한 주사위를 던질 때 6개의 값 1~6은 각각 확률 1/6을 갖는다.사건의 확률은 사건을 만족시키는 결과의 확률의 합으로 정의된다. 예를 들어, "다이롤링 짝수 값" 사건의 확률은 다음과 같다.

반대로 랜덤 변수가 연속체에서 값을 취하면 일반적으로 개별 결과는 확률 0을 가지며 구간과 같이 무한히 많은 결과를 포함하는 사건만 양의 확률을 가질 수 있습니다.예를 들어, 슈퍼마켓에서 햄 한 조각의 무게를 측정하고 저울에 정밀도가 많은 자릿수가 있다고 가정합니다.십진수가 0이 아닐 가능성이 높기 때문에 정확히 500g의 무게는 0입니다.그럼에도 불구하고 품질 관리에서 햄 "500g" 포장의 무게는 최소 98% 확률로 490g에서 510g 사이여야 하며, 이러한 요구는 측정 기기의 정확성에 덜 민감하다.

절대 연속 확률 분포는 여러 가지 방법으로 설명할 수 있습니다.확률밀도함수는 주어진 값의 극소확률을 나타내며, 결과가 주어진 구간에 있을 확률은 해당 ^[5]구간에 걸쳐 확률밀도함수를 통합함으로써 계산할 수 있습니다.분포에 대한 또 다른 설명은 누적 분포 함수를 사용하는 것입니다. 누적 분포 함수는 랜덤 변수가 특정 값($x$의 경우 < $)\displaystyle$ P$(X$ <x))\$displaystyle$P(X$<x$)\)$$보다 크지 않을 가능성을 나타냅니다.누적분포함수는 오른쪽 ^[6]그림과 같이 확률밀도함수${\displaystyle }$- ${\$ {\$displaystyle -\infty }$ ~$x{\displaystyle }$ {\$displaystyle$ x$\}$의 영역입니다.

일반 확률 정의

확률분포는 확률질량함수 또는 누적분포함수 등 다양한 형태로 기술할 수 있다.하나는 가장 일반적인 설명의 절대적으로와 이산 연속 변수에 대한 적용되는 확률 함수의 P:에 의한→ R{\displaystyle P\colon{{A\mathcal}}\to\mathbb{R}}의 입력}한{\displaystyle{{A\mathcal}space}는 표본 공간에 레를 준다 related[해명 필요한]이다.알 수 확률그 ^{[citation needed]}출력으로.

P(앞면) = 0.5, P(뒷면) = 0.5가 되도록 $함수{\displaystyle }$ $P(\displaystyle$ P$)$를 정의한 코인 던지기 예시와 같이 확률 $함수{\displaystyle }$P(\$displaystyle$ P$)$는 샘플 공간 자체의 부분 집합으로 취할 수 있다.하지만, 이 숫자(예를 들어, R{\displaystyle \mathbb{R}}, N{\displaystyle \mathbb{N}})의 집합으로 표본 공간 변화시키는 확률 변수의 광범위한 사용 때문에, 더 세트(수 세트)[7]고 모든 프로의 이러한 특정한 종류의 주장은 하위 집합 확률 분포를 공부하는 것이 일반적이다.영혼이 문서에서 설명하는 효용도 분포는 이 유형입니다.$일반적$으로 변수$$X의$$ 특정 값이 특정 $(\displaystyle$$$E$)$^[4][8]에 속할 가능성을 P${\displaystyle (Xe}$E$$)(\$displaystyle$ P$(X\in$ E$)$로 $나타냅니다{\displaystyle }$.

위의 확률 함수는 모든 Kolmogorov 공리를 충족하는 경우에만 확률 분포를 특성화합니다. 즉, 다음과 같습니다.

1. ${\displaystyle P}$( ${\displaystyle X\mathrm{eE}}$ )${\displaystyle }$0 ${\displaystyle 0\mathrm{}\mathrm{eE}}$ A \ $displaystyle$P ($X$ \ $in$ E ) \ $geq$ 0 \ ;\$forall$E \$in$ \ $mathcal${ $A$} the the$$。따라서 확률은 음이 아닙니다.
2. ${\displaystyle P}$( ${\displaystyle X\mathrm{eE}}$ ${\displaystyle )\le }$ ${\displaystyle 1\mathrm{}\mathrm{eE}}$ A \ $displaystyle$P ($X$ \ $in$ E ) \$leq$ 1 ; \ $forall$E \$in$ \ $mathcal${ $A$} $。$따라서 1을$초과$할 가능성은 없습니다$.$
3. ${\displaystyle }$${\displaystyle P_{}}$${\displaystyle }$( ${\displaystyle X}$ ${\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{i}}$ ${\displaystyle \underset{}{}{}_{}{i}_{}}$ )$$ {$displaystyle$( $X$\ $in$\ $bigsq cup$_ {$i$ ) = \$sum _${ i } $P$ ( X \ $in$ _ { i } )${\displaystyle }$= \ sum _ { i $}$ P ( X \ in E _ { i$$} ) } } $style$ 、 { i _ $display$style 。

확률 함수의 개념은 확률 공간$({\displaystyle X,}$ ${\displaystyle A,}$ $)$의 요소(X,${\mathcal$$${$A}, P$로 정의함으로써 더욱 엄격해집니다. $여기$서$$X(\$displaystyle$ X$)$는 가능한 결과의 $집합$이고$,$ \$displaystyle(\$displaystyle {$A})$은 모든 $eDISPLAYSTYLE$의 ${\displaystyle \mathrm{집합}}$입니다${\displaystyle .}$}의$$ 측정가능성, $P{\displaystyle }${\$displaystyle$ P$$$}$는 각 측정가능 $서브셋{\displaystyle }$ E${\displaystyle a\mathcal{}}$ $A$^[9]$in$ \mathcal {A}}에 확률을 할당하는 확률함수 또는 확률측도입니다$.$

확률 분포는 일반적으로 두 가지 클래스 중 하나에 속합니다.이산 확률 분포는 가능한 결과의 집합이 이산(예: 동전 던지기, 주사위 굴림)이고 확률이 결과의 확률의 이산 리스트에 의해 부호화되는 시나리오에 적용할 수 있다. 이 경우 이산 확률 분포는 확률 질량 함수라고 알려져 있다.한편, 절대 연속 확률 분포는 가능한 결과의 집합이 특정일의 온도와 같은 연속 범위(예: 실수)의 값을 취할 수 있는 시나리오에 적용할 수 있다.절대 연속적인 경우 확률은 확률밀도함수에 의해 기술되며 확률분포는 정의상 확률밀도함수의 ^[4][5][8]적분이다.정규 분포는 일반적으로 절대적으로 연속적인 확률 분포입니다.연속 시간에 정의된 확률적 과정을 포함하는 것과 같이 더 복잡한 실험은 보다 일반적인 확률 측정의 사용을 요구할 수 있다.

표본 공간이 1차원인 확률 분포(예: 실수, 레이블 목록, 순서 레이블 또는 이진수)를 일변량이라고 하며 표본 공간이 2차원 이상의 벡터 공간인 분포를 다변량이라고 합니다.일변량 분포는 단일 랜덤 변수가 다양한 값을 취할 확률을 제공하고 다변량 분포(공동 확률 분포)는 두 개 이상의 랜덤 변수 목록인 랜덤 벡터가 다양한 값의 조합을 취할 확률을 제공합니다.중요하고 일반적으로 발생하는 일변량 확률 분포에는 이항 분포, 초기하 분포 및 정규 분포가 포함됩니다.일반적으로 발생하는 다변량 분포는 다변량 정규 분포입니다.

확률함수 외에 누적분포함수, 확률질량함수 및 확률밀도함수, 모멘트발생함수 및 특성함수도 기초가 되는 누적분포함수를 ^[10]일의적으로 결정하므로 확률분포를 식별하는 역할을 한다.

용어.

확률 분포에 관한 문헌에서 널리 사용되는 몇 가지 핵심 개념과 용어는 다음과 같다.^[1]

기본 용어

• 랜덤 변수: 표본 공간에서 값을 가져오며, 확률은 어떤 값과 값 집합을 더 많이 취할지 나타냅니다.
• 사건: 특정 확률로 발생하는 랜덤 변수의 가능한 값(출력) 집합입니다.
• 확률 함수 또는 확률 척도: 이벤트 $E{\displaystyle ,}$\$displaystyle$ E$,\$^[11]$displaystyle$ P$(X\in$ E$)$가 발생할 확률$$ $X$ ${\displaystyle x}$E$)$를 나타냅니다$$.
• 누적분포함수: X$(실제값$ 랜덤 변수만 해당)가 X$$$(표시$ 스타일$$$$X$)$ 이하의 값을 취할 확률을 평가하는 함수입니다.
• 분위수 함수: 누적 분포 함수의 역함수입니다.$(displaystyle$ x$)$는 x$(displaystyle$ x$)$를 $넘지{\displaystyle }$ 않을 $($$displaystyle$q$)$로 지정합니다.

이산 확률 분포

• 이산 확률 분포: 최종 또는 셀 수 있는 값이 무한히 많은 많은 랜덤 변수의 경우.
• 확률 질량 함수(pmf): 이산 랜덤 변수가 일부 값과 같을 확률을 제공하는 함수입니다.
• 빈도 분포: 표본에서 다양한 결과의 빈도를 표시하는 표입니다.
• 상대 도수 분포: 각 값이 샘플의 여러 결과(예: 샘플 크기)로 분할(정규화)된 도수 분포.
• 범주형 분포: 값의 집합이 유한한 이산 랜덤 변수의 경우.

절대 연속 확률 분포

• 절대 연속 확률 분포: 셀 수 없이 많은 값을 가진 많은 랜덤 변수의 경우.
• 확률 밀도 함수(pdf) 또는 확률 밀도: 표본 공간(랜덤 변수가 취할 수 있는 값의 집합)에서 주어진 표본(또는 점)의 값이 해당 표본과 같을 수 있는 상대적 가능성을 제공하는 함수로 해석될 수 있습니다.

관련 용어

• 지지: 랜덤 변수가 0이 아닌 확률로 가정할 수 있는 값 집합입니다.랜덤 $변수{\displaystyle }$ X$(\displaystyle$ X$)$의 경우 R $(\$로 표시될 수 있습니다.
• 꼬리:^[12] pmf 또는 pdf가 상대적으로 낮은 경우 랜덤 변수의 경계에 가까운 영역입니다.보통 X> { $display style$ X > $a$}, < { $displaystyle X$< b } 또는 그 조합의 형태를 .
• Head:^[12] pmf 또는 pdf가 상대적으로 높은 지역.보통 a< < \ $displaystyle$a \$X$ \ b입니다.
• 기대치 또는 평균: 확률을 가중치로 사용한 가능한 값의 가중 평균 또는 연속 아날로그.
• 중위수: 중위수보다 작은 값 집합과 중위수보다 큰 값 집합이 각각 1/2 이하의 확률을 갖는 값입니다.
• 모드: 이산 랜덤 변수의 경우 확률이 가장 높은 값, 절대 연속 랜덤 변수의 경우 확률 밀도 함수에 로컬 피크가 있는 위치.
• 양분위수: $q-quantile$은 $값{\displaystyle }$x{$displaystyle$x}입니다. P( < ) $=$q { $displaystyle$ P$(X<x$)=$q$입니다.
• 분산: 평균에 대한 pmf 또는 pdf의 두 번째 모멘트, 분포의 산포를 측정하는 중요한 측도입니다.
• 표준 편차: 분산의 제곱근이며, 따라서 분산의 또 다른 측도입니다.
• 대칭성: 특정 값의 왼쪽에 있는 분포 부분(일반적으로 중앙값)이 오른쪽에 있는 부분의 거울 이미지인 일부 분포의 속성입니다.
• 왜도: pmf 또는 pdf가 평균의 한쪽으로 "기울어진" 정도를 측정한 값입니다.분포의 세 번째 표준화된 순간입니다.
• 첨도: pmf 또는 pdf의 꼬리의 "뚱뚱함"을 나타내는 척도입니다.분포의 네 번째 표준화된 순간입니다.

누적분포함수

실수치 랜덤 변수의 특수한 경우 확률분포를 확률측도 대신 누적분포함수로 등가적으로 나타낼 수 있다.$확률분포{\displaystyle }$ p$\displaystyle$ p$\$displaystyle$$X의$$누적분포함수는 다음과 같이 정의한다.

모든 실수값 랜덤 변수의 누적 분포 함수에는 다음과 같은 특성이 있습니다.

• $)$ {$displaystyle$ F$(x)}$은(는) 감소하지 않습니다.
• $)$ {$displaystyle$ F$(x)}$는 우측 연속형입니다.
• ${\displaystyle 0f}$F (${\displaystyle x}$ )${\displaystyle 1}$1 \ $displaystyle$ 0 \ $leq$F ($x$ ) \ $leq$1$$;
• ${\displaystyle \underset{}{lim}}$ x ${\displaystyle \underset{}{\to }}$ -${\displaystyle \underset{}{\mathrm{}}}$F (${\displaystyle x}$ ) ${\displaystyle =}$ { $displaystyle \lim$_ {$x$ \$to$- \ $infty } F$ ( x ) = ${\displaystyle 0}$$$} 및$$ ${\displaystyle \underset{}{lim}}$ x ${\displaystyle \underset{}{\to }}$ ${\displaystyle \underset{}{\mathrm{\infty }}\underset{}{}}$ (${\displaystyle x}$ ) ${\displaystyle =}$ 1$${ $displaystyle \lim$_ {$x$ \ $to$\ $infty } F$ ( x )$$$= 1$ ;
• ( < b ) () -F () { $displaystyle \ Pr$ ($a$ <$X$ \ $leq$ b ) $= F ( b$)}

반대로 위의 특성 중 처음 4개를 만족하는 $함수{\displaystyle }$F : ${\displaystyle R\mathbb{}}$ ${\displaystyle \to }$ {\$displaystyle$ F$:\mathbb {R}$ \$to \mathbb {R}}$은 실수에 대한 ^[13]확률 분포의 누적 함수이다.

확률분포는 이산분포,^[14] 절대연속분포 및 단일연속분포의 합으로 분해할 수 있으며, 따라서 누적분포함수는 3개의 누적분포함수의 합으로 분해를 허용한다.

이산 확률 분포

이산확률분포란 카운트 가능한 값의 수만을^[15] 취할 수 있는 랜덤변수의 확률분포입니다(거의 확실하게).^[16] 즉, $이벤트{\displaystyle }$ E$(\displaystyle$ E$)$의 확률은 (유한 또는 카운트할 수 있는 무한) 합으로 표현될 수 있습니다.

$여기$서 A$(\displaystyle$ A$)$는 카운트 가능한 세트입니다.따라서 이산 랜덤 변수는 확률 질량 ${\displaystyle }$p (${\displaystyle x}$ ) ${\displaystyle =P}$ ( ${\displaystyle X}$ ${\displaystyle =x}$) {$displaystyle$ p$(x$)=$P(X=x$를 갖는 변수입니다. 값의 범위가 셀 수 있을 정도로 무한할 경우, 이러한 값은 0으로 감소해야 확률이 1이 될 수 있습니다.예를 들어 p${\displaystyle }$(${\displaystyle n)}$ ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle 2}$$$n ({ $displaystyle$$$p (n) ${\displaystyle =}$ $1$.$2$.${\displaystyle }$.${\displaystyle }${$2$$$^ { $n$}$$} )일 $경우{\displaystyle }$$,$ 확률의 합계는${\displaystyle }1{\displaystyle \mathrm{}}$/$2$+${\displaystyle 1}$ / ${\displaystyle 4\mathrm{}}$+ ${\displaystyle 4}$+ ${\displaystyle 1\mathrm{}}$ / 8 + 8 + 1 / 8 + 1 / 8 + 1 / 8 + 1 / 1 / 1 / 1 / 1 / 1 / 1 / 1 / 1 / 8 + 1 / 8 $11$ / 8 ${\displaystyle \cdots }$1 / 8 $⋯$1 / 8 ⋯1 / 8 ⋯ 1 ⋯1 / 8 $41$ / 1 ⋯1 / 1 ⋯${\displaystyle 1}$ / 8${\displaystyle }$⋯1 / 8$$

이산 랜덤 변수는 확률 분포가 이산인 랜덤 변수입니다.

통계 모형화에 사용되는 잘 알려진 이산 확률 분포에는 포아송 분포, 베르누이 분포, 이항 분포, 기하 분포, 음이항 분포 및 범주 ^[3]분포가 포함됩니다.더 큰 모집단에서 표본(관측치 집합)을 추출하면 표본 점에는 이산형이며 모집단 분포에 대한 정보를 제공하는 경험적 분포가 있습니다.또한 이산 균등 분포는 다수의 선택 사이에서 등확률 랜덤 선택을 하는 컴퓨터 프로그램에서 일반적으로 사용됩니다.

누적분포함수

실수값 이산 랜덤 변수는 점프의 불연속성에 의해서만 누적 분포 함수가 증가하는 랜덤 변수로 동등하게 정의될 수 있다. 즉, cdf는 더 높은 값으로 "점프"하는 경우에만 증가하며 점프가 없는 구간에서 일정하다.점프가 발생하는 지점은 정확히 랜덤 변수가 취할 수 있는 값이다.따라서 누적분포함수는 다음과 같은 형태를 갖는다.

cdf 점프가 이루어지는 포인트는 항상 계수 가능한 세트를 형성한다. 이는 계수 가능한 집합이 될 수 있으며, 따라서 실수의 밀도가 높을 수도 있다.

디랙 델타 표현

이산 확률 분포는 종종 결정론적 랜덤 변수의 확률 분포인 Dirac 측도로 표현됩니다.결과$$$\delta {\displaystyle }$(\$displaystyle \obe$에 $대해{\displaystyle {}_{}}$$δ$(\displaystyle $\obe$ _${\obe$$\})$에 집중된 Dirac 측정값으로 합니다. 이산 확률 분포가 주어지면 P$X$∈${\displaystyle }$A ) $=$ $(\displaystyle$A$)$인$계수$ $집합$이 있습니다.ass $함수{\displaystyle }$p(\$displaystyle$ p$).$ E$(\displaystyle$ E$)$가 이벤트인 경우

요컨대

마찬가지로 이산분포는 Dirac 델타함수를 일반화 $확률밀도함수{\displaystyle }$ f$\backslash$$displaystyle$f로 나타낼 수 있습니다.

즉,모든 $이벤트{\displaystyle }$E$.\{displaystyle$ E$.}.$

표시기 기능 표현

이산 랜덤 $변수{\displaystyle }$ X$(\displaystyle$ X$)$의 경우, ${\displaystyle {u\mathrm{}}_{}{}_{}}$ , ${\displaystyle {u\mathrm{}}_{}}$1 , $...$ (\$displaystyle u_{0}$ , $u_{$1} , \$dots$} 를$$ 0 이외의 확률로 사용할 수 있는 값으로 $합니다{\displaystyle {}_{}}$.나타내다

이들은 분리 집합이며, 이러한 집합의 경우

따라서 X$({displaystyle$X})가 ${\displaystyle {}_{}{}_{}}$0 ,${\displaystyle {u\mathrm{}}_{}}$1 , $...({displaystyle u_{0$} $,$u_${1$} , \$dots$} $이외$의 값을 취할 확률은 0이므로 X$({displaystyle$X})를 다음과 같이 쓸 수 있습니다.

확률 0의 집합($여기$서 ${\displaystyle 1_{}}$ A$(\$은 A$(\displaystyle$ A$)$의 표시 함수)를 제외한다. 이는 이산 랜덤 변수의 대체 정의 역할을 할 수 있다.

원포인트 분포

특수한 경우는 하나의 고정 값만 취할 수 있는 랜덤 변수의 이산 분포입니다. 즉, 결정론적 분포입니다.형식적으로 표현하면${\displaystyle ,}$ $랜덤{\displaystyle }$ 변수$$X(\$style$ X$)$는 $가능$한 결과$$x(\$display style$x$$${\displaystyle )}$ $=$ 1. (\$style$P(X{=}x)=$1.}$ 기타$$^[18] 가능한 모든 결과는 확률 0이 $된다{\displaystyle }$.누적 분포 함수는 0에서 1로 즉시 점프합니다.

절대 연속 확률 분포

절대 연속 확률 분포는 실선의 전체 구간과 같이 셀 수 없을 정도로 많은 가능한 값을 가진 실수에 대한 확률 분포이며, 어떤 사건의 확률을 ^[19]적분으로 표현할 수 있습니다.보다 정확하게 말하면, 실제 랜덤 $변수{\displaystyle }$X({$displaystyle$ X$}$는 각${\displaystyle }$구간 [${\displaystyle a,}$ b]${\displaystyle r\mathbb{}}$ R$({$$infty$})\mathbb {R$}\to$ [0${\displaystyle ,\backslash }$infty$])\mathbb$ R$({a,b$})\displaystyle [a,\mathb}R$}\$mathb$}\$mathb}의$$$$ 함수$:[$가 있는 경우 절대 연속 확률 분포를 갖는다.[ ${\displaystyle a}$, $]$\ $displaystyle [ a$ , $b$]에$$ 속하는 $tyle$X는$$I \ $displaystyle$I 위의 $f\backslash$^[20][21]$displaystyle$의 적분에 의해 지정됩니다.

이것은 확률밀도함수의 정의이므로 절대 연속 확률분포는 확률밀도함수가 있는 분포와 정확히 일치합니다.특히 X$(\displaystyle$ X$)$가 임의의 $단일{\displaystyle }$ 값$displaystyle$ a$)(\$$displaystyle$ a$\leq$을 취할 확률은 0입니다. 왜냐하면 상한과 하한이 일치하는 적분은 항상 0이기 때문입니다.간격 $[{\displaystyle a,}$ $]$ {$style [$a, b] {style [a,$b]$가 측정 가능한 $세트{\displaystyle }$A {$style$ A$\}$로 대체되어도 그에 따른 등식은 유지됩니다.

절대 연속 랜덤 변수는 확률 분포가 절대 연속인 랜덤 변수입니다.

절대 연속 확률 분포에는 정규 분포, 균일 분포, 카이 제곱 분포 등 여러 가지 예가 있습니다.

누적분포함수

위에서 정의한 절대 연속 확률 분포는 정확히 절대 연속 누적 분포 함수를 가진 분포입니다.이 경우 $누적분포함수{\displaystyle }$F(\$displaystyle$ F$)$는 다음과 같은 형태를 갖는다.

$여기$서$$f {\$displaystyle$f$$}는 분포$$P {\$displaystyle$ P$\}$에 대한 랜덤 $변수{\displaystyle }$X {\$displaystyle$ X$}$의 밀도입니다.

용어에 관한 주의:절대 연속 분포는 연속 누적 분포 함수를 갖는 연속 분포와 구별되어야 한다.모든 절대 연속 분포는 연속 분포이지만 그 반대는 사실이 아닙니다. 절대 연속 분포도 이산 분포도 혼합 분포도 아니고 밀도가 없습니다.예를 들어 칸토어 분포가 있습니다.그러나 일부 저자는 누적 분포 함수가 절대 연속인 모든 분포를 나타내기 위해 "연속 분포"라는 용어를 사용한다. 즉, 절대 연속 분포를 연속 ^[4]분포라고 한다.

밀도 함수와 이와 동등한 절대 연속 측정에 대한 보다 일반적인 정의는 절대 연속 측정을 참조하십시오.

콜모고로프 정의

확률론의 측정이론 공식화에서 랜덤 변수는 확률공간$δ$ ${\displaystyle F,P\mathbb{}}$)(\$displaystyle(\$Omega, {\$mathcal {F},$ \$mathbb {P})$에서 측정가능공간$X$ $)$ {\$mathcal {P})$까지의 $측정가능함수{\displaystyle }$X({$styleX})$로 정의된다.$\}$에서 {\$displaystyle$$\{\Omega\mid$ X$(\obega$)\mid X(\obega$)\in$ 형식의 사건 확률이 콜모고로프의 확률 공리를 만족하는 경우 X$\displaystyle$X의$$ $확률{\displaystyle }$ 분포는 ${\displaystyle {}_{}}$이다$.$는 X$a$P ${\displaystyle =}$ ${\displaystyle P{}^{}}$X -$$ \ $mathbb { P$}$$$=$ \ $mathbb$ { P } = \ $mathbb$ { P } X^ { - 1 }$$= \ $mathbb${ P } X^ { - $1$$$} = \ mathbbb { P } X^ { - { - 1 $\}$^[22][23][24] $\}{\displaystyle }$ 의 $확률$ 측도입니다.

기타 분포

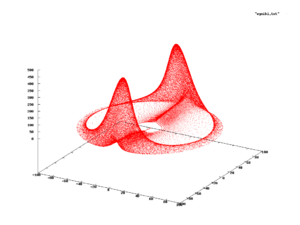
R $(\$ $또는$ $(\$^{$k})$을 $지원$하는 절대적으로 연속적이고 이산적인 분포는 하이퍼큐브 또는 볼과 같은 비교적 단순한 하위 집합에서 지원되므로 수많은 ^[4][6]현상을 모델링하는 데 매우 유용하다.그러나 항상 그렇지는 않으며, 실제로 복잡한 곡선을 이루는 $지지대$가 있는 현상은 R$$n \${\displaystyle {}^{}}$ style $\display$ : $[a, b]$ ${\displaystyle \to }$ ${\displaystyle {}^{}}$n \$rightarrow \mathbb {R} ^{n}$ 등의$$$$ $공간{\displaystyle {\mathbb{}}^{}}$ R n \$display$style \$mathbb {R}$^{$n}$ }이 경우 확률분포는 그러한 곡선의 이미지에서 지지되며,^[25] 그에 대한 닫힌 공식을 찾는 것이 아니라 경험적으로 결정될 가능성이 높다.

오른쪽 그림에 한 가지 예가 나타나 있으며,^[26] 플라즈마에서 랭뮤어파의 거동을 모델링하는 데 사용할 수 있는 미분 방정식(일반적으로 라비노비치-파브리칸트 방정식) 시스템의 진화를 보여준다.이 현상을 연구할 때 부분 집합에서 관찰된 상태는 빨간색으로 표시됩니다.따라서 빨간색 부분 집합의 특정 위치에서 상태를 관찰할 확률은 얼마인지 물어볼 수 있습니다. 그러한 확률이 존재한다면,^[27][25] 시스템의 확률 측도라고 불립니다.

이러한 복잡한 지원은 동적 시스템에서 자주 나타납니다.시스템에 확률 측정이 있다고 단정하는 것은 간단하지 않으며, 주된 문제는 다음과 같습니다.${\displaystyle {t\mathrm{}}_{}}$ 1${\displaystyle {}_{}{}_{}}$ ${\displaystyle {t\mathrm{}}_{}}$ 2${\displaystyle {}_{}{}_{}}$ ${\displaystyle {t\mathrm{}}_{}}$ 3$${ { $display$ style $t$_ { $1$\ $ll$t$$_ {$}$ \ $ll$$$ t _ {$$} $o{\displaystyle }$ and o$$oO를 지원의 $서브셋$으로 합니다.시스템에 확률 측정이 존재하는 경우 설정$O{\displaystyle }$(\ $displaystyle$ $O$$)$ 내의$$ 상태를 관찰하는 빈도는${\displaystyle {t1\mathrm{}}_{}}$, 2 )로 동일합니다.$\displaystyle [t_{1$}, $t_{2}}$ 및${\displaystyle }$[${\displaystyle {t\mathrm{}}_{}}$ 2,${\displaystyle {}_{}{}_{}}$ $]$ {$displaystyle [t_{2$}, $t_{3$ 예를 들어, t ${\displaystyle \mathrm{\to }}$${\displaystyle }${$displaystyle$ $\sin(t)}$이$($${\displaystyle 가}$$)$ \$arfty$}일$$ 때 $한계$가 \$displaystyle$ t$\rightyle$ converge \arfty $}$와 ${\displaystyle \mathrm{유사}}$하게 진동할 수 있습니다.공식적으로 이 측정치는 시스템이 무한한 ^[28]미래로 관찰될 때 상대 주파수의 한계가 수렴되는 경우에만 존재합니다.확률 측정의 존재를 연구하는 동적 시스템의 한 부문은 에르고드 이론이다.

이러한 경우에서도 확률 분포가 존재하는 경우, 각각 지지대가 셀 수 없거나 셀 수 없는지에 따라 "절대 연속" 또는 "이산"으로 칭할 수 있습니다.

난수생성

대부분의 알고리즘은 숫자$X{\displaystyle }$(\$displaystyle$ X$)$를 생성하는 의사 난수 생성기를 기반으로 하며, 숫자 X(\displaystyle X)는 하프 오픈 간격[0, 1)에서 균일하게 분포됩니다.그런 다음 $이러한{\displaystyle }$ 랜덤 변수$$X(\$displaystyle$ X$)$를 몇 가지 알고리즘을 통해 변환하여 필요한 확률 분포를 갖는 새로운 랜덤 변수를 생성합니다.이 균일한 의사 랜덤성의 소스에서는 임의의 랜덤 변수의 실현을 ^[29]생성할 수 있습니다.

예를 들어 U$${\$displaystyle$ U$$$}$의 분포가 0과 1 사이라고 $가정$합니다.< < \ $displaystyle$0 <$p$ < $1$의 임의의 Bernouli 변수를 작성하려면 다음과 같이 정의합니다.

하도록

이 랜덤 변수 X는 $모수{\displaystyle }$p\$displaystyle$ p$\}$^[29]를 가진 베르누이 분포를 가지고 있습니다. 이것은 이산 랜덤 변수의 변환입니다.

절대 연속 랜덤 변수의 분포 $함수{\displaystyle }$F {\$displaystyle$ F$}$는 절대 연속 랜덤 변수를 구성해야 한다.${\displaystyle F^{}}$$(\displaystyle$ F$)$의 역함수인 ${\displaystyle {\mathit{Fi}}^{}}$ n$$ {\$mathit {inv}}$은$($는) 균일한 $변수{\displaystyle }$U(\$displaystyle$ U$):$

예를 들어 지수 $분포{\displaystyle }$ F${\displaystyle (x}$ ${\displaystyle )}$ $=$- ${\displaystyle {\delta }^{}}$ x$${\$display style$ F$(x$)=$1-e^{-\lambda$x}}인$$ 랜덤 변수를 생성해야 한다고 가정합니다.

$따라서{\displaystyle {}^{}}$ ${\displaystyle {\mathit{Fi}}^{}}$ ${\displaystyle {\mathit{n}}^{}}$v (${\displaystyle u}$ ) ${\displaystyle =\frac{}{}}$ - ${\displaystyle \frac{1}{}}$ ${\displaystyle \ln }$ in $1$ -${\displaystyle u}$） { $displaystyle$ F^ { \ $mathit${ $inv$} =$flac${ -$1 displayda }$${\displaystyle }$} \ ln ( 1 -$$u )$$if$$$$ if ${\displaystyle 、}$ ${\displaystyle \mathrm{U}}$（ ${\displaystyle 0}$ , $1 ）$ $u$ u x x x x x $x{\displaystyle }$ 、 X 。${\displaystyle }${\$displaystyle$ X$=F^{\mathit {inv}}(U$)=$blac${-$1}{\displayda }}\ln(1-U$$이{\displaystyle }$ 분포는 $"\displaystyle\lambda$^[29] 입니다.

통계 시뮬레이션(몬테카를로 방법)에서 자주 발생하는 문제는 주어진 방식으로 분포된 의사 난수의 생성이다.

공통 확률 분포 및 그 응용 프로그램

확률 분포와 그들이 설명하는 랜덤 변수의 개념은 확률 이론의 수학적 분야와 통계학의 기초가 된다.인구에서 측정할 수 있는 거의 모든 값(예: 사람 키, 금속의 내구성, 매출 성장, 교통 흐름 등)에는 확산 또는 가변성이 있다. 거의 모든 측정은 본질적인 오류로 이루어진다. 물리학에서는 가스의 운동 특성에서 양자 역학에 이르기까지 많은 과정이 확률적으로 설명된다.기본 입자의 교정 기술.이러한 이유와 다른 여러 가지 이유로 인해 단순한 숫자가 수량을 설명하는 데 적합하지 않은 경우가 많지만 확률 분포가 더 적합한 경우가 많습니다.

다음은 관련된 공정 유형별로 그룹화된 가장 일반적인 확률 분포의 목록입니다.자세한 목록은 검토 중인 결과의 특성(이산, 절대 연속, 다변량 등)별로 그룹화하는 확률 분포 목록을 참조하십시오.

아래의 모든 일변량 분포는 단일 정점에 있습니다. 즉, 값이 단일 점 주위에 군집화되어 있다고 가정합니다.실제로 실제로 관측된 수량은 여러 값 주위에 군집화될 수 있습니다.이러한 양은 혼합물 분포를 사용하여 모형화할 수 있습니다.

선형 성장(예: 오류, 오프셋)

• 정규 분포(가우스 분포), 이러한 단일량에 대해 가장 일반적으로 사용되는 절대 연속 분포

지수적 성장(물가, 소득, 인구 등)

• 로그 정규 분포(로그가 정규 분포된 단일 수량에 대한 로그 정규 분포
• Pareto 분포, 로그가 기하급수적으로 분포되는 단일 수량에 대한; 원형 멱함수 법칙 분포

균등하게 분포된 수량

• 유한한 값의 집합에 대해 이산 균일한 분포(예: 공정 다이의 결과)
• 절대 연속 분포 값을 위한 연속 균일한 분포

베르누이 시행(예/없음, 주어진 확률로 사건 발생)

• 기본 분포:
  • 단일 베르누이 시행 결과에 대한 베르누이 분포(예: 성공/실패, 예/아니오)
  • 이항 분포 - 고정된 총 독립 발생 횟수(예: 성공, 찬성 투표 등)에 대해
  • 음의 이항 분포, 이항형 관측치의 경우이지만 관심 있는 수량은 주어진 성공 횟수가 발생하기 전의 실패 횟수입니다.
  • 이항형 관측치의 경우지만 관심 있는 수량이 첫 번째 성공 이전의 실패 횟수인 기하 분포; 음이항 분포의 특수한 경우
• 한정된 모집단에 걸친 샘플링 방식 관련:
  • 고정 횟수의 총 발생 횟수에 대한 "양수 발생"(예: 성공, 찬성 투표 등)에 대한 초기하 분포, 대체되지 않은 표본 추출 사용
  • 총 발생 횟수가 고정된 경우 "긍정 발생 횟수"(예: 성공, 찬성 투표 등)에 대한 베타 이항 분포는 폴랴 항모형을 사용하여 표본 추출한다(어떤 의미에서는 대체되지 않은 표본 추출의 "반대").

범주형 결과(K개의 가능한 결과가 있는 사건)

• 단일 범주형 결과에 대한 범주형 분포(예: 조사에서 예/아니오/아마도); 베르누이 분포의 일반화
• 고정된 수의 총 결과가 주어진 범주형 결과의 각 유형에 대한 다항 분포; 이항 분포의 일반화
• 다변량 초기하 분포, 다항 분포와 유사하지만 대체하지 않고 표본 추출 사용, 초기하 분포의 일반화

포아송 공정(지정된 비율로 독립적으로 발생하는 사건)

• 포아송 분포 - 지정된 기간 동안 포아송 유형 사건의 발생 횟수에 대한 분포
• 지수 분포 - 다음 포아송 유형 사건이 발생하기 전의 시간
• 다음 k개의 포아송 유형 사건이 발생하기 전의 시간에 대한 감마 분포

정규 분포 성분이 있는 벡터의 절대값

• Rayleigh 분포 - 가우스 분포 직교 성분을 사용하여 벡터 크기를 분포합니다.레일리 분포는 가우스 실수 성분과 허수 성분이 포함된 RF 신호에서 찾을 수 있습니다.
• 쌀 분포, 정지 백그라운드 신호 성분이 있는 경우 Rayleigh 분포의 일반화입니다.멀티패스 전파에 의한 Rician 페이딩 및 0이 아닌 NMR 신호의 노이즈 파손이 있는 MR 이미지에서 볼 수 있습니다.

제곱합으로 연산된 정규 분포 수량

• 카이 제곱 분포, 표준 정규 변수의 제곱합에 대한 분포. 예를 들어 정규 분포 표본의 표본 분산에 대한 추론에 유용합니다(카이 제곱 검정 참조).
• 표준 정규 변수의 비율과 척도화된 카이 제곱 변수의 제곱근의 분포인 학생 t 분포. 분산을 알 수 없는 정규 분포 표본의 평균에 대한 추론에 유용합니다(학생 t-검정 참조).
• F-분포, 두 척도 카이 제곱 변수의 비율 분포. 예를 들어 분산 비교 또는 R-제곱(상관 계수 제곱)을 포함하는 추론에 유용합니다.

베이지안 추론의 공역 사전 분포로서

• 단일 확률(0과 1)에 대한 베타 분포, 베르누이 분포 및 이항 분포에 공역
• 감마 분포, 음이 아닌 척도 모수의 경우 포아송 분포 또는 지수 분포의 속도 모수, 정규 분포의 정밀도(역분산) 등에 활용됩니다.
• 디리클레 분포, 합계가 1이어야 하는 확률 벡터에 대해 범주형 분포 및 다항 분포에 활용; 베타 분포의 일반화
• Wishart 분포(대칭 비음수 유한 행렬의 경우), 다변량 정규 분포의 공분산 행렬의 역행렬에 활용; 감마^[30] 분포의 일반화

확률 분포의 일부 특수 응용 프로그램

• 특정 단어 및 단어 시퀀스의 발생 가능성을 할당하기 위해 자연어 처리에 사용되는 캐시 언어 모델 및 기타 통계 언어 모델은 확률 분포를 통해 그렇게 한다.
• 양자역학에서, 주어진 지점에서 입자를 찾을 확률 밀도는 그 지점에서 입자의 파동 함수의 크기의 제곱에 비례합니다(본 규칙 참조).따라서, 입자의 위치의 확률 분포 함수는 $P_{}$ a$x_{}$ x$b_{}$b ($t$ ) $={}_{}^{}$ a $d$ x$\psi \mathrm{}$ ( $x$,$t$ ) ${}^{\mathrm{}}$ ($textstyle P_{a\leq$x\$leq$ b } ( t) = \$int _{$a}^$b}$\, \$Psi ( x$ ,$t$ ) $^2}${$$} ' ' ' { 。3차원에 적분되어 있습니다.이것은 양자역학의 ^[31]핵심 원리이다.
• 전력 흐름 연구에서 확률론적 부하 흐름은 입력 변수의 불확실성을 확률 분포로 설명하고 확률 ^[32]분포 측면에서 전력 흐름 계산을 제공한다.
• 열대성 사이클론, 우박, 사건 간 시간 ^[33]등의 이전 빈도 분포를 기반으로 한 자연 현상 예측

「 」를 참조해 주세요.

• 조건부 확률 분포
• 공동확률분포
• 준가동성 분포
• 경험적 확률 분포
• 히스토그램
• 확률론에 대한 리만-슈틸테스의 적분 응용

리스트

• 확률 분포 목록
• 통계 토픽 리스트

레퍼런스

인용문

원천

외부 링크

• "Probability distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 연속 확률 분포 필드 가이드, Gavin E.사기꾼들.